MATEMATIKA STAROG EGIPTA

Brojni sistem

Jedna od najstarijih velikih civilizacija i kultura što ih je čovek stvorio na zemlji bila je staroegipatska. I danas ćemo se još uvek naći zadivljeni pred ostacima te velike baštine rasute po muzejima po svetu i u svojoj postojbini: reč je o nedostižnim umetničkim delima u muzeju u Kairu. Na primer zbirke nađene u Tutankamonovoj grobnici, ostaci čudesne građevine kraljice Hačepsut ili velikih piramida ili dešifrovani tekstovi iz staroegipatske knjige mrtvih ili grobnice u Dolini kraljeva.
Čudesnu lepotu i mudrost egipatske civilizacije otkrivamo iz mnogobrojnih zapisa uklesanih na stenama hramova, na kamenim sarkofazima i iz ispisanih tekstova svih mogućih vrsta (koji su sačuvani zahvaljujući suvoj egipatskoj klimi), pomoću hijeroglifa koje je prvi put dašifrovao Šampolion, 1824. i 1826. godine. On je srećnim slučajem okolnosti došao do jedne rozete-kamena na kom je bio ispisan tekst na egipatskom, grčkom i latinskom jeziku. Zahvaljujući tome, život i zbivanja, pa i staroegipatska matematika dobro su poznati danas.
O staroegipatskoj matematici najviše saznajemo iz dva papirusa : jedan je tzv. Ahmesov ili Rhindov papirus koji se čuva u Londonu (iz vremena oko 1650. godine pre naše ere), a sadrži 85 matematičkih problema na svitku papirusa širokom oko 30 cm i dugačkom 6 cm.
Drugi je tzv. moskovski (čuva se u Moskvi, a iz vremena je oko 1850. godine pre naše ere), sadrži 25 matematičkih problema na svitku papirusa širokom oko 8 cm, a dugačkom 6 cm.
"Egipat je dar Nila", jer bez blatnjave žute vode koja je značila život ne bi se razvila ni bogata civilizacija starog Egipta. Posle redovnih velikih poplava Nila svake bi se godine granice zemljišnih poseda lako izbrisale i trebalo ih je ponovo odrediti. Valjalo je dakle premeriti zemljišta, a da bi se to realizovalo neophodna su bila znanja iz matematike, posebno geometrije.
Izgradnja velikih piramida i veličanstvenih hramova i grobnica pretpostavljala je obimna geometrijska znanja koja su Egipćani morali posedovati.
Kao ilustraciju snage i "matematičke" preciznosti staroegipatskog građevinarstva spomenimo veliku piramidu kod Gize (sagrađenu pre 5000 godina) u koju je ugrađeno više od dva miliona kamenih blokova teških 2-3 tone, dovučenih sa suprotne strane Nila. Plafoni komore u piramidi su od granitnih blokova teških po 54 tone, donesenih iz kamenoloma udaljenih od mesta gradnje oko 1000 km, a sastavljenih jedan uz drugi tako precizno da između dva susedna ne možemo staviti nokat.Začuđuju i podaci da je strana ove piramide prema polovini piramidine visine jednaka broju p=3.16 (kada se ima na umu da su posle čitavih 1500 godina broj p računa kao tri cela onda je ova vrednost još više za divljenje). Ulaz u prvu odaju ove čuvene piramide je pod uglom koji tačno odgovara geografskoj širini mesta na kom je piramida podignuta. Egipćani su se (kao i Vavilonci) bavili vrlo mnogo astronomijom. Imali su svoj kalendar u kome su godine delili na 12 meseci, a mesec na 30 dana. Poznavali su i astronomsku godinu koja se od kalendarske razlikovala za 6 časova. Posle 1460. godine poklapao se dan astronomske i kalendarske godine.
Egipćani nisu znali za kontinuirano računanje vremena, pa su oni svoju istoriju podelili na vece vremenske odlomke koji se podudaraju sa vladavinom pojedinih dinastija. Međutim, u piramidama su pronađeni dokazi o znanjima starih Egipćana i iz područija astronomije, što je opet siguran dokaz da su bili dobro upoznati sa mnogim matematičkim istinama.
Egipćani su u početku koristili hijeroglife za cifre. Imali su znake za 1, 10, 100, 1000, 10000, 100000, 1000000, 10000000. "Jedan" se označavalo vertikalnim potezom, "deset" potkovicom, "sto" mernim užetom, "hiljadu" listom lotosa (koji u hiljadama prekriva jezera), "deset hiljada" guštericom (kojih je posle poplava Nila bilo na desetine hiljada u zamuljenim obalama).
Često su upotrebljavali i druge znake. "Sto" su nekad obeležavali slikom palmove grančice, "hiljadu" cvetom krina ili slikom lampe itd.
Egipatski matematičari su se služili dekadnim sistemom, što verovatno potiče od brojanja na prste. Brojevi 1,2,3,4 mogli su se jednostavno i sugestivno predstaviti redom sa : 1,11,111,1111. Takav je postupak očito neodrživ za velike brojeve. Prva ideja o zapisu većih brojeva koja se nametnula, bilo je tzv. “aditivno notiranje brojeva”. Odabrani su posebni znakovi za pojedine “istaknute” brojeve i njihovim nizanjem
označavali su se proizvoljni brojevi. Ti “istaknuti” brojevi  bili su prirodno stepeni broja 10, jer su se koristili dekadnim sistemom brojeva.
Zapišimo neki konkretan broj na opisani način :

212547

• 2 gušterice (za 200000)
• 1 prst (za 10000)
• 2 lista lotosa (za 2000)
• 5 savijenih užeta (za 500)
• 4 potkovice (za 40)
• 7 poteza (za 7)

Ideja je dakle aditivnog ili sabirnog načina pisanja brojeva u tome da je vreednost niza znakova jednaka zbiru vrednosti svih znakova koji čine niz. Stari Egipćani su redovno znakove nizali s desna u levo, pa bi se tako gledali i znakovi za manje dekadne jedinice. Budući da mi, naprotiv, pišemo s leva u desno, običaj je da se tako pišu i transkripcije staroegipatskih hijeroglifskih zapisa.
Zanimljivo je da je postojao i poseban hijeroglifski znak za “beskonačno”. Svakako ne za beskonačno veliki broj u nekom modernom smislu, već za broj koji je toliko veliki da ga je, kako im se činilo, nemoguće izraziti nekim zapisom. Npr. za broj poput “broja zrnaca peska” ili “broj kapi vode” u moru. Hijeroglif za takav pojam bio je slika čoveka sa uzdignutim rukama i pogledom usmerenim u nebo.
Osim navedanih upotrebljavali su se povremeno i posebni znaci za neke brojeve koji nisu dekadne jedinice : goveđi tragovi (2), morska zvezda sa pet krakova (5), ljudska glava (7), skica tri kraka kose (30), itd.

Razlomci

 Posebno je zanimljivo kako su stari Egipćani označavali razlomke, tim pre što u tome ne nalazimo sličnosti ni u jednoj drugoj kulturi, ni u jednom drugom narodu. To je bila neka njihova specifična izmišljotina u kojoj su bili vrlo spretni.
Razlomak sa brojiocem 1 označavao se tako da se ispred znaka za imenilac stavljao poseban hijeroglif sa značenjem “deo”. Takvi razlomci su bili osnovni, a svi ostali razlomci (sa brojiocem različitim od 1) svode se na osnovne. Jedine izuzetke činili su razlomci 1/2 i 2/3, za koje su postojali posebni hijeroglifi.
Svođenje razlomaka na zbir osnovnih izvodilo se pomoću tablica koje su sadržale razlaganje razlomaka oblika 2/n tj. jedino potrebno razlaganje pošto se množenje svodilo na udvostručavanje. U Rhindovom papirusu nalaze se tablice koje sadrže razlaganje na osnovne razlomke za sve neparne brojeve od 5 do 101.
Zanimljivo je da u pomenutim tablicama ima rastava koje nisu egzaktne tj. u kojima zbir osnovnih nije sasvim tačan, ali je vrlo približno jednak polaznom razlomku koji se rastavlja na osnovne.
Uopšte princip po kome se vrši svođenje razlomaka na osnovne razlomke nije jasan (npr. za n=19 osnovni razlomak je 12 76 114, a ne 12 57 220). Ovaj princip sa razlomcima karakteriše egipatsku matematiku kao glomaznu i razvučenu ali uprkos tim preprekama rad sa osnovnim razlomcima upotrebljavao se hiljadama godina i to ne samo tokom grčkog perioda nego čak i u srednjem veku. U to vreme ovo razlaganje razlomaka pretpostavljalo je određenu matematičku veštinu, a postoje i interesantne teorije koje objašnjavaju na koji način su Egipćani dolazili do rezultata.

Algebra

 Rhindov papirus sadrži i određenu matematičku simboliku. Postoje znakovi koji odgovaraju našem " = " i oznake za "nepoznatu”, " + " je označeno hijeroglifom para nogu što idu s desna u levo, a " – " je označeno hijeroglifom para nogu što idu s leva u desno.
Interesantno je kako su množili prirodne brojeve. Ta metoda odaje da su se izgleda nekada služili binarnim sistemom. Tu metodu ćemo najlakše pokazati na primeru:

 Želimo da pomnožimo 7 sa 12.
Postupili bi ovako: 1 * 12 = 12
2 * 12 = 24
4 * 12 = 48
Budući da je 1 + 2 + 4 = 7 biće
7 * 12 = 1 * 12 + 2 * 12 + 4 * 12 =
= 12 + 24 + 48 = 84

 Drugim rečima, množitelj se predstavi kao zbir stepena od 2, zatim se uzastopnim udvostručavanjem množitelja dobiju proizvodi tih stepena sa množiteljem i konačno se saberu odgovarajući parcijalni proizvodi.
Kako god nam taj način množenja izgledao nespretan, pa čak i primitivan moramo uzeti u obzir da stari Egipćani nisu imali razvijen pozicioni način pisanja brojeva, koji su tek mnogo kasnije iz Indije u Evropu preneli Arapi.
Egipćani nisu poznavali matematiku kao, strogu, egzaktnu nauku, već se ona sastojala od uzoraka pojedinih vrsta računa. Jedan primer iz moskovskog papirusa to potvrđuje. On je označen kao problem br.6 i glasi:

  Ako ste zapitani za lik od 12 koji ima širinu koja je 3/4 dužine, morate podeliti 1 sa 3/4 . Rezultat je 1 1/3. Uzmite sada ovaj 12 puta 1 1/3, pa je rezultat 16. Sada morate naći broj koji pomnožen sam sa sobom daje 16, pa je rezultat 4 za dužinu, a za širinu je 3/4 od toga, naime 3.

 Uporedimo ovo egipatsko rešenje sa savremenim:

 x, y – stranice pravougaonika
P = 12 – površina pravougaonika 
y = 3/4* x Kako je P = x * y , biće :
12 = x * 3/4x ili x2 = (1:3/4) *12
ili x2 = 16 , x = 4
x = 4
Pošto je y = 3/4 x imamo da je y = 3/4 * 4, pa je
y = 3

 U savremenom rešenju polazi se od formule za izračunavanje površine pravougaonika koja je predhodno dokazana, pa rešenje počiva na čvrstim logičkim razlozima, dok u egipatskom postupku nema nikakvog logičkog obrazloženja takvog postupka. Zato je egipatko rešenje radno pravilo za postupanje u sličnoj situaciji.
Ipak, ne može se sa punom sigurnošću odbaciti svaka mogućnost da je možda ipak u nekih staroegipatskih matematičara postojala i klica drugačijeg gledanja na matematiku. Naime, ne treba zaboraviti da npr. Ahmesov papirus nije bio namenjen nekim profesionalnim matematičarima, već prvenstveno zemljoradnicima i trgovcima. Ne bi bilo tako čudno da je autoru tog sačuvanog rukopisa bilo više stalo do toga da svoje čitaoce nauži kako će nešto izračunati, nego da im dokazuje ispravnost svoje tvrdnje.
Dva sačuvana papirusa sadrže mnogo problema vezanih za jednačine prvog stepena sa jednom nepoznatom. Za obeležavanje nepoznate u jednačini upotrebljavao se hijeroglif koji znači “ gomila “, npr. HAU ili AHA. Zato se egipatska algebra naziva “ AHA-RAČUN “.
Evo nekoliko primera :
U 26. zadatku papirusa stoji :
Koji broj uvećan za njegovu četvrtinu daje 15 ?
Egipćani su to rešili uvodeći “ metodu lažnog rešenja “, što je vrlo značajno. Uzeli su da je x = 4, prva aproksimacija u jednačini :
x + x/4 = 15
F (x) = C
x = x1
F (x1) = C1
C=C1
Ako ovo nije onda :
x: x1 = C : C1
x = C/C1 * x1
Pošto je 4 + 4/5 ¹ 5 imamo da je :
x : x1 = 15 : 5
x = 15/5 * 4
x= 12

 Ahmesov papirus počinje rečima :
Propisi da se dospe do saznanja nejasnih stvari ... za vlade Gornjeg i Donjeg Egipta Ra-a-us-a ... po ugledu na stare spise ovaj je spis sastavio Ahmes.
Te reči tj. deo da se dospe do saznanja svih nejasnih stvari   dolaze do izražaja u sledećim primerima :
Da se 700 hlebova podeli na 4 lica, tako da jedno dobije 2/3,drugo 1/2.
Ako bi se zadatak shvatio kao što je napisan, bila bi to nelogičnost, pošto 2/3 i 1/3 već čine 700. Dakle prvo i treće lice bi razdelilo sve hlebove, a za drugo i četvrto ništa ne bi ostalo. Međutim Ahmes pokušava da reši taj zadatak tako što traži broj čiji će zbir gornjih razlomaka biti :
2/3 + 1/2+ 1/3 + 1/4 = 21/12 traženi broj 700.
Dakle :
2/3 * x + 1/2 * x + 1/3 * x+ 1/4* x= 700 ili 21/12 * x = 700
x = 400
Jer 21/12 * 400 = 700.
Egipćani su poznavali aritmetičke i geometrijske progresije, što se vidi u jednom od poslednjih problema Rhindovog papirusa :
Neko imanje sadrži 7 zgrada. U svakoj od njih je 7 mačaka. Svaka od njih uhvati po 7 miševa, od kojih je svaki pojeo 7 zrnaca pšenice. Svako bi zrno moglo dati 7 merica žita. Koliko bi na imanju bilo ukupno zgrada, mažaka, miševa, zrna pšenice i merica pšenice ?
 Rešenje :

• zgrada 7
• mačaka 49
• miševa 343
• zrna 2401

 19607

Egipćani su znali i ta svojstva aritmetičkog reda. Evo jednog takvog primera iz Rhindovog papirusa :
Podeli 100 hlebova na 5 ljudi, tako da količina koje će primiti čine aritmetičku sredinu. Sedmina zbira triju najvećih obroka trebalo bi da je jednaka zbiru dvaju najmanjih.
Rešenje savremenim metodama je sledeće:
x + (x + d ) + (x + 2d ) + (x + 3d ) + (x + 4d ) = 100
1/7 ((x + 4d ) + (x + 2d ) + (x + 3d ) = x + (x + d )
odnosno sređeno :
x + 2d = 20
11 * x= 2d
x = 5/3 , d= 55/6,
pa obroci iznose :
5/3, 65/6, 20, 175/6, 115/3.

Geometrija

 U svojoj “knjizi” Ahmes se bavi izučavanjem površine jednakokrakog trougla i trapeza po obrascima koji su i danas u upotrebi :

 P = ( a * h ) / 2

 R = ( a + b ) / 2 * h

 Do skora se smatralo da je i Ahmes, kao što su i pisci mnogo kasnijeg doba, računao ove površine po netačnim obrascima:
P = a * b / 2
P = ( a + c ) / 2 * h
Na jednoj strani hrama u Edesu postoje i sačuvani zapisi o izračunavanju površine trapezoida, dakle bilo kakvog četvorougla. Prevedeni na naš matematički jezik, oni ističu da takav lik sa parovima naspramnih stranica, dužine a i c, odnosno b i d, imaju površinu izraženu formulom :

P = a + c / 2 * b + d / 2

 Za četvorouglove koji ne odstupaju mnogo od pravougaonika, graška te formule je gotovo zanemarljiva. Slično, i staroegipatska formula za izračunavanje površine kruga je bila samo približna, ali i kao takvadobra.Približnost se u tom slučaju sastojala u tome da su umesto broja koji mi danas označavamo p i koji je približno 3.14, stari Egipćani upotrebljavali četvorostruki kvadrat od 8/9, koji je približno jednak 3.16. Njihova je formula, dakle, bila pogrešna za manje od 1%.

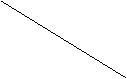
 d/6 d/9
 

 d = prečnik
P0 = d2 , P0 = 4 * d2 / 4 , p = 4 - velika greška
P1 = P0 – 4 * (d /6) = d2 – d2 /9 = (1 – 1/9) * d2
P1 = 8/9 * d2

 P2 = P1 – 8 * (d / 9)2 = 8/9 * d2 – 8/9 * 9 * d2
P2 = (1 – 1/9) * 8/9 * d2 = (8/9)2 * d2
P2 =( 8/9) * d2 = 4 * (8/9)2 * d2/ 4
p = 4 * 64/81 a to je približno 3.1602 

 Egipćani su imali i vrlo približne formule za izračunavanje zapremine kugle, a tačnu formulu za izračunavanje zapremine piramide. Uprevo je među najzanimljivijim delovima moskovskog papirusa njegov 14. Problem :
Ako ti je rečeno : zarubljena piramida visine 6, sa stranicom donje osnove 4 i stranicom gornje 2. Kvadriraj taj 4, to je 16. Udvostruči 4, to je 8. Kvadriraj 2, to je 4. Saberi ovo 8 i 16 i 4, to je 28. Uzmi 28 puta 2, to je 56. Vidi 56 je! Vidiš to je ispravno.
To očito odgovara računanju zapremine zarubljene piramide prema egzaktnoj formuli :
V = ( a2 + a*b + b2 ) * h/3
Izvlačenje kvadratnog korena ne nalazi se kod Ahmesa, ali ga ima u jednom drugom papirusu , koji je nađen u Kahunu, južno od piramida. U jednom papirusu koji se čuva u Berlinu ima ovakav zadatak :
Rastavi 400 u 2 kvadrata čije su strane u odnosu 2 : 1 ½.
Dakle :
X2 + Y2 =400
X : Y = 2 : 11/2odatle je
X2 : Y2 = 4 : 2 1/4
Pomoću pokušaja iz ovoga se izvodi : X2 = 4,
  Y2 = 2 1/4, i dalje
X2 + Y2 = 6 1/4 ili VX2 + Y2 = V 61/4 =1/2
  Ali je V X2 + Y2 = V 400 = 20

 20 : 2 1/2= 8.
Tim putem se izračunava vrednost za :
X = 8 *2 = 16 , a za Y = 8 * 1 1/2 = 12
Ovim se putem došlo do jednačina
82 + 62 = 102 , 162 + 122 = 202
koje su postale iz :
42 + 32 = 52
Stari Egipćani postavljali su hramove kao i piramide u pravcu istok-zapad. Obavljanje tog posla smatralo se za največu svetinju i tajnu. Vršili su ga članovi dinastije i sveštenici. Pri tom su se koristili znanjem iz astronomije i geometrije. Na jednom takvom hramu urezane su reči faraona koji ga je zivao : Uzeh kolac i malj. Držah jedno uže zajedno sa boginjom Sateh (boginja Sateh je bila zaštitnica biblioteka i temelja). Pogled mi je tražio hod zvezda. Kad moje oči pogledaše na sazvežđe Velikog Medveda i proteče određeni deo vremena, zabodoh ga na ugaonu tačku Tvoga doma Gospode. To je isto učinila i boginja Sateh na drugom kraju užeta. Tako je bio utvrđen meridijan tj. pravac sever-jug. Da bi utvrdili pravac istok-zapad stari Egipćani su se služili užetom od 12 mernih jedinica. To uže su podelili čvorovima na tri dela, tako da je prvi deo imao 3, drugi 4, a trći 5 dužnih jedinica.
Ako se zategnuto uže utvrdi za zemlju kočićima u tačkama B i C, pa se sastave krajnje tačke užeta A i D i zategnu po zemlji sa pravim uglom u

 B, onda će ove tri duži AB, BC, CD činiti pravougli trougao. Prava AB je normalna na BC, a to je pravac istok-zapad u kome je hram postavljen.

 A 
 

 
B C

 Drugim rečima Egipćani su znali za poseban slučaj Pitagorine teoreme, mada neki “kritički orijentisani” savremeni istoričari matematike to osporavaju, u smislu da nema direktnog dokaza da su stari Egipćani pravoulost trougla sa stranicama 3,4,5 povezivali sa jednakošću : 32 + 42 = 52.

Šta još reći o starim Egipćanima i njihovoj matematici , sem izraziti divljenje prema jednom takvom narodu i njihovoj kulturi , koja je svakako bila kamen temeljac za sveukupni razvoj čovečanstva, osim možda još istaći da po svemu što do danas znamo o staroegipatskoj matematici čini se da su je oni shvatali kao, našim rečnikom rečeno, empirijsku matematiku. Nije bilo pokušaja da se izvede neka formula ili da se dokaže neka teorema, već se na primerima ilustruvalo kako ih treba upotrebljavati. Npr. za izračunavanje površina ili zapremina davali su određeni recept, prema kome treba postupati bez obrazloženja zašto su takvi kakvi su. Drugim rečima, stari Egipćani, čini se, matematiku nisu shvatali kao deduktivnu nauku. Takav program ostvaren je tek u starogrčkoj matematici i to u Pitagorejskoj školi, gde njihova razmišljanja (teoreme) da broj 2 nije racionalan, predstavlja prvu teoremu koja ne samo Grčku, već i sveukupnu matematiku izvodi iz sfere praktičnog.
Kao jedna posledica takvog gledanja na matematiku u starom Egiptu, ogleda se u tome da se nije činila načelna razlika između tačnih, egzaktnih formula i samo približnih, aproksimovanih formula i metoda računanja. Ipak, i te posledice, koje su bile samo približne, zadovoljavale su potrebe gde su bile primenjivane.
Svakako je najčešća primena matematike u starom Egiptu bila npr. u vođenju poreske evidencije i u komercijalnim poslovima. Tu se kod njih često nalaze računi sa brojevima reda veličine stotina hiljada, tj. brojevima koje bi smo u našem pozicionom zapisu označavanja pisali kao šestocifrene.
U jednom zapisu iz vremena oko 3100. godine pre nove ere o nekom vojnom poduhvatu, navode se u hijeroglifskim znakovima brojevi reda veličine više miliona tj. u našem zapisu sedmocifreni brojevi.
Jedan od najvećih autoriteta za staroegipatsku matematiku, Neugebaner, napisao je u jednom svom delu:

 Egipatska tehnika računja, koja se u prvi mah čini poput neke smese najveće primitivnosti i začuđujuće komplikovanosti računa, pokazuje se potpuno jednostavnom i u sebi zatvorenom celinom. Tako se dakle može reći da je egipatska matematika jedini sačuvani čisti primer računske tehnike koja je bila vrlo razvijena, koja u čitavom svom razvoju nije doživela nikakvog bitnog diskontinuiteta, većse zaista još u potpunosti temelji na najranijoj osnovi računanja, naime na brojanju i na individualnim pojmovima razlomaka.

  LITERATURA :

 1. “Matematika kroz vekove i civilizacije” Vladimir Devide

 2. “Sve o matematici” Lanselot Hogben

 3. “Kratak pregled istorije matematike” Dirk J. Strojk

 4. “Razvoj matematike” Žarko Dadić

 preuzmi seminarski rad u wordu » » » 

Besplatni Seminarski Radovi