OSTALI SEMINARSKI RADOVI
IZ MATEMATIKE: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
GRUPE SIMETRIJA PRAVILNIH POLIEDARA
SIMETRIJE LIKOVA PROSTORA E³
Sama rec simetrija potice od grcke reči Sin-sa-metron sto znaci meriti skladno. Neki anticki filozofi smatrali su simetrije zakonitostima koje se odredjuju unutar drugih podrucja:lepotom se bavi iskljucivo estetika - tvrdili su pritom.U tim polemikama se izdvajaju uglavnom dva misljenja:-harmonija je bozanskog porekla : smisao idealnog je coveku nedostupan...
-matematika je najpozvanija da operise tim pojmovima. Aristotel u svom delu "Metafizika" kaze: "Lepota je zakonitost čiji su kriterijumi bazirani na matematickim principima". A Platon:" Najsavrsenija lepota najbliža je lepoti geometrijskih tela ".
Pod pojmom simetrije podrazumevala se samerljivost, svaki sklad delova unutar jedne figure ili medju raznim figurama, dok je asimetrija znacila nesamerljivost.
KLASIFIKACIJA IZOMETRIJSKIH TRANSFORMACIJA PROSTORA E³
Radi izvodjenja potpune klasifikacije prostora E³ i detaljnijeg poznavanja
simetrija , neophodno je dobro poznavati ravansku refleksiju i njene osobine
jer se sve ostale izometrijske transformacije prostora definisu pomocu
ravanske refleksije.
Sledece teoreme govore o svim postojecim izometrijskim transformacijama
prostora E³. Navescu ih bez dokaza.
Teorema 1. Svaka izometrijska transformacija I prostora E³ moze se predstaviti kao kompozicija konacnog broja ravanskih refleksija.Minimalan broj nije veci od cetiri.
Teorema 2. Svaka direktna izometrijska transformacija
Iprostora E³ moze se predstaviti kao kompozicija dveju
osnih simetrija E³.
Teorema 3. (Bernuli-Salova) Svaka direktna
izometrijska transformacija prostora E³ predstavlja koincidenciju, translaciju
ili rotaciju.
Teorema 4. Svaka indirektna transformacija prostora E³ je ravanska , rotaciona ili klizajuca refleksija.
Teorema 5. Svaka indirektna izometrijska transformacija
prostora E³ koja ima jedinstvenu invarijantnu tacku O predstavlja rotacionu
refleksiju sa sredistem O.
Prethodne teoreme omogucavaju da klasifikaciju izometrijskih transformacija
euklidskog prostora E³ prikazemo u obliku sledece sheme:
Direktne: Indirektne:
Koincidencija Ravanska refleksija
Translacija Osnorotaciona
refleksija
Osna rotacija Klizajuca refleksija
Zavojna kretanja
Razlikujemo sedam vrsta izometrijskih transformacija, pa s obzirom na
to razlikujemo i sedam vrsta simetrija i likova u tom prostoru, a to su:
Koincidencija, ravanska simetrija, osna simetrija reda n, osnorotaciona
simetrija reda n, translaciona simetrija, klizajuca simetrija, zavojna
simetrija.
Sa ovako utvrdjenim postojecim vrstama simetrija likova u prostoru E³,
moze se pristupiti nalazenju postojecih grupa simetrija u prostoru E³.
Definicija. Simetrijom nekog lika F u prostoru E³ zovemo svaku izometrijsku transformaciju I tog prostora takvu da je I(F)=F. Skup svih simetrija lika F E³ obrazuje grupu, koju zovemo gupom simetrija tog lika i oznacavamo sa GI(F).
U geometriji pravilnih poliedara u prostoru E posebnu paznju privlace pitanja koja se odnose na njihove grupe simetrija. Sledecim teoremama ustanovice se sve postojece simetrije tih poliedara. Dokazace se tri teoreme; prva-kojom ce biti ustanovljen red grupe simetrija pravilnih poliedara, druga-kojom ce biti identifikovane sve postojece simetrije iz grupe rotacija, i treca-identifikovace se sve preostale simetrije tih poliedara.
Teorema 1. Ukupan broj svih postojecih simetrija
pravilnog poliedra u prostoru E³ jednak je dvostrukom broju njegovih ivicnih
uglova, tj.
cetvorostrukom broju njegovih ivica. Polovina tih simetrija ne menja orijentaciju
lika, a druga polovina menja.
Dokaz: neka su <ABC i <A'B'C' ma koja dva ivicna ugla pravilnog
poliedra F, i neka je O njegovo srediste. Tacke O, A, B, C i O, A', B',
C' su nekomplanarne, pri cemu je:
(O, A, B, C) podudarno (O, A', B', C') i (O, A, B,C) podudarno (O,C',B',A'),
te postoje I1 i I2, dve izometrijske transformacije prostora E³ od kojih
jedna, na primer I1, preslikava O,A,B,C redom u O,A',B',C', a druga iste
tacke O,A,B,C slika O,C',B',A'. Jedna od tih transformacija je direktna,
druga indirektna i u odnosu na njih lik je invarijantan tj:
I1(F)=F, I2(F)=F.
Ovo je tacno, jer u transformaciciji I1 pljosni (ABC....H) odgovara pljosan
(A'B'C'...H'), a iz podudarnosti svih diedara i pljosni lika F, zakljucuje
se da u transformaciji I1 susednim pljosnima sa (ABC...H) odgovaraju pljosni
susedne sa (A'B'C'...H') itd. za sve odgovarajuce susedne pljosni. Na
potpuno identican nacin zakljucuje se da je I2(F)=F.
Svaka od izometrijskih transformacija I1 i I2 predstavlja simetriju poliedra
F. Svakom ivicnom uglu pridruzuje se jedna direktna i jedna indirektna(izometrijska
transformacija) simetrija, zbog cega je njihov ukupan broj jednak dvostrukom
broju ivicnih uglova tj cetvorostrukom broju ivica.
Pravilan poliedar u prostoru E³ kome pljosni imaju po m stranica , a
rogljevi po n ivica ima red grupe simetrija koji se moze izraziti jednakostima:
RED G(IF) = 2mp+2nt =4i, gde su p broj pljosni, t je broj temena a i je
broj ivica tog poliedra.
Teorema 2. Red grupe rotacija pravilnog poliedra
, jednak je dvostrukom broju njegovih ivica. Simetrije ove grupe sastoje
se od osnih rotacija
oko pravih koje sadrze sredista pljosni i upravne su na njima; pravih
odredjenih sredistima naspramnih ivica i pravih koje predstavljaju ose
rogljeva tog poliedra.
Dokaz: Neka je rec o pravilnom poliedru F kome pljosni imaju
po m stranica, rogljevi po n ivica koji ima t temena, i ivica i p pljosni.
Zna se da je ukupan broj svih simetrija poliedra F jednak 4i, a broj simetrija
koje ne menjaju njegovu orijentaciju je 2i. Po Bernuli-Salovoj teoremi
direktne transformacije prostora E³ su: rotacije, translacije, zavojna
kretanja i koincidencija. Kako je rec o nuldimenzionoj grupi simetrija
kojima transformacije imaju zajednickih invarijantnih tacaka, moze se
govoriti samo o prvoj i zadnjoj transformaciji- rotaciji i identicnom
preslikavanju. Tacnije, grupa direktnih simetrija pravilnog poliedra F
sastoji se od koincidencije i jedne od sledecih osnih rotacija:
1.Osne rotacije definisane u odnosu na prave koje sadrze sredista pljosni
poliedra F i upravne su na njima.
Ove rotacije preslikavaju svako teme neke pljosni u sva ostala temena
iste pljosni. Znaci ukupan broj tih rotacija je m-1.
Ako pravilan poliedar nema naspramnih pljosni, a tu je jedini tetraedar,
onda su prave upravne na dvema razlicitim pljosnima u njihovim sredistima
razlicite medju sobom. Rotacije oko ovih pravih razlikuju se medju sobom,
pa je njihov ukupan broj (m-1)p, tj za tetraedar osam. Svi ostali pravilni
poliedri imaju po p/2 parova naspramnih pljosni. Ose upravne u sredistima
dveju naspramnih pljosni su istovetne, te su i rotacije oko njih istovetne.
Zbog toga je ukuan broj postojecih rotacija oko pravih upravnih na pljosnima
u njihovim sredistima jednak (m-1)p/2 za sve pravilne poliedre sem tetraedra.
2.Osne rotacije definisane u odnosu na sredista naspramnih ivica.
Svaka takva prava je osa samo jedne rotacije-osne simetrije. Kako svaki
pravilan poliedar ima ½ naspramnih ivica , ukupan broj rotacija oko pravih
odredjenih sredistima naspramnih ivica je i/2.
3.Osne rotacije definisane u odnosu na prave koje su ose rogljeva posmatranog
pravilnog poliedra.
Rotacija oko svake od ovih pravih prevode jednu pljosan roglja i na koju
drugu pljosan tog istog roglja. Kako tih pljosni ima n-1, ukupan broj
rotacija oko prave koja predstavlja osu jednog roglja pravilnog poliedra
je n-1.Ose razlicitih rogljeva razlicite su medju sobom, sem kod pravilnog
tetraedra, pa su razlicite i rotacije oko njih.
Svaki pravilan poliedar , sem naravno tetraedra, ima t/2 parova naspramnih
temena. Ose rogljeva kod tih temena su istovetne, rotacije oko osa istovetne,
pa je ukupan broj postojecih rotacija oko svih mogucih takvih osa jednak
(n-1)t/2.
Kod pravilnog tetraedra, ose ma kog roglja upravne su na naspramnim pljosnima
u njihovim sredistima , pa se poistovecuju sa osama iz slucaja 1, pa se
odgovarajuce rotacije poistovecuju.
Teorema 3. Ukupan broj simetrija pravilnog
poliedra koje menjaju njegovu orijentaciju jednak je dvostrukom broju
ivica tog poliedra. Skup svih
simetrija sastoji se iskljucivo iz rotacionih i ravanskih refleksija.
Dokaz: Neka opet bude rec o pravilnom poliedru, kome rogljevi imaju
po n ivica, koji ima p pljosni , sa po m stranica , t temena ,i ivica
. Sve (indirektne transformacije) simetrije ovog poliedra koje mu menjaju
orijentaciju iscrpljene su sa dve vrste ravanskih i tri vrste rotacionih
refleksija:
1.Ravanskom refleksijom definisanom bisektralnim ravnima unutrasnjih diedara, poliedra F. Simetralne ravni naspramnih unutrasnjih didara se poklapaju u svim (ostalim) pravilnim poliedrima, samo su razlicite u pravilnom tetraedru. Ukupan broj ovih ravanskih refleksija je kod tetraedra jednak broju njegovih ivica, a kod ostalih pravilnih poliedara i/2. Kod pravilnog oktaedra simetralna ravan unutrasnjeg diedra poklapa se ne samo sa istom naspramnog, vec i sa simetralnom ravni onih dvaju diedara kojima ivice pripadaju bisektralnoj ravni polaznog diedra. Zbog toga pravilan oktaedar ima samo i/4 posmatranih ravanskih refleksija, tj svega 3.
2.Ravanskom refleksijom definisanom medijalnim ravnima ivica poliedra
F.
Medijalne ravni ivica mogu se preklapati sa bisektralnim ravnima unutrasnih
diedara, kao na primer u pravilnom tetraedru, dodekaedru I ikosaedru.
Kod pravilnog heksaedra i oktaedra to nije slucaj, ali se kod njih medijalne
ravni nekih ivica poklapaju medju sobom.Pravilan heksaedar ima samo tri
medijalne ravni ivica,jer se medijalne ravni njegovih naspramnih ivica
poklapaju.
3.Rotacionim refleksijama definisanim u odnosu na prave odredjene sredistima
naspramnih pljosni.Ove rotacione refleksije prevode svako teme jedne od
dveju naspramnih pljosni,na primer W, u odgovarajucim temenima druge pljosni
W1, pa postoji i takva refleksija koja slika svako teme u njemu naspramno.
Ta rotaciona refleksija predstavlja centralnu simetriju poliedra. Kao
je m paran broj sto je slucaj jedino kod pravilnog heksaedra, ravanska
refleksija definisana u odnosu na zajednicku osnovu svih tih rotacionih
refleksija slika jednu pljosan W u njoj naspramnu W1. Zbog toga je ukupan
broj rotacionih refleksija definisanih u odnosu na prave odredjene sredistima
dveju naspramnih pljosni, sem u slucajevima kada one predstavljaju centralnu
ili ravansku refleksiju, jednak m-1 (m neparno), tj m-2 (m parno). Kako
tetraedar uopste nema naspramnih pljosni, on uopste nema rotacionih refleksija.
Svi ostali pravilni poliedri imaju p/2 parova naspramnih pljosni, pa je
ukupan broj rotacuionih refleksija oko pomenutih osa (opet izuzimajuci
slucaj kada one predstavljaju centralnu ili ravansku refleksiju) jednak
(m-1)p/2, odnosno (m-2)p/2 zavisno od m.
4.Rotacionim refleksijama definisanim u odnosu na prave koje spajaju
sredista naspramnih ivica.
Kod svih pravilnih poliedara, sem tetraedra, naspramne ivice su komplanarne
pa se ne mogu definisati rotacione refleksije oko ovih osa koje bi bile
razlicite od centralne ili ravanske refleksije. Naspramne ivice pravilnog
tetraedra su nekomplanarne, pa postoje dve rotacione refleksije definisane
pravom odredjene njihovim sredistima. Niedna od ovih rotacionih refleksija
ne predstavlja centralnu ili ravansku refleksiju.Ukupan broj im je 6,
jer pravilan tetraedar ima tri para naspramnih ivica. Sredista svih ovih
rotacionih refleksija poklapaju se (sa sredistem tetraedra).
5.Rotacionim refleksijama definisanim u odnosu na prave odredjene naspramnim
temenima.
Ove rotacione refleksije prevode svaku ivicu koja polazi iz jednog (od
tih dvaju temena) u svaku ivicu koja polazi iz drugog od tih dvaju temena.
Moze se pritom desiti da se ivice koje polaze iz prvog temena preslikaju
u sebi naspramne ivice koje polaze iz drugog temena-tada je rec o rotacionoj
refleksiji – koja predstavlja centralnu simetriju. Ili pak , kakav je
slucaj jedino kod pravilnog oktaedra, da ravanska refleksija definisana
u odnosu na zajednicku osnovu svih ovih rotacionih refleksija, prevodi
ivice koje polaze iz prvog temena u ivice koje polaze iz drugog temena.
Zbog svega ovog, ukupan broj rotacionih refleksija definisanih u odnosu
na prave koje spajaju naspramna temena izuzimajuci, naravno, slucajeve
centralne I ravanske refleksije jednak je (n-1), n neparno tj (n-2), n
je parno.
Svi pravilni poliedri (sem tetraedra), imaju t/2 naspramnih temena , pa
se ukupan broj pomenutih rotacionih refleksija svodi na (n-1)t/2, za neparno,
tj (n-2)t/2 za parno n. Pravilan tetraedar uopste nema naspramnih temena
pa se razumljivo kod njega ni ne definisu ove rotacione refleksije.
Prethodnim teoremama ustanovljene su sve postojece vrste simetrija pravilnih poliedara.
PRAVILNI TETRAEDAR
Pravilan tetraedar ima 24 simetrije od kojih jedna polvina menja njegovu orijentaciju, a druga ne.
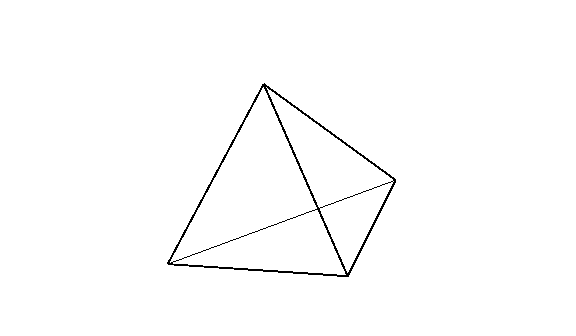
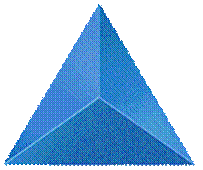
Direktne transformacije bile bi: 8 osnih rotacija reda tri definisanih
u oba smera u odnosu na prave odredjene visinama tog tetraedra. Tri osne
simetrije reda dva definisane su u odnosu na prave odredjene sredistima
naspramnih ivica.
Indirektne transformacije kod pravilnog tetraedra bile bi: 6 ravanskih
refleksija definisanih bisektralnim ravnima α unutrasnjih diedara I 6
rotacionih refleksija reda cetiri definisanih u oba smera u odnosu na
prave odredjene sredistima naspramnih ivica o i ravan W. To je I jedina
rotaciona refleksija kojom raspolaze, jer pravilan tetraedar nema ni naspramnih
pljosni ni naspramnih temena.
PRAVILAN HEKSAEDAR
Pravilan heksaedar ima 48 simetrija od kojih jedna polovina menja orijentaciju,
a druga ne.
Direktne izometrijske transformacije I koje se mogu definisati kod pravilnog
heksaedra takve da vazi I(F)=F su:
6 osnih simetrija reda cetiri definisanih u odnosu na prave koje spajaju
sredista naspramnih pljosni I tro osne simetrije reda dva definisane u
odnosu na iste prave;
6 osnih simetrija reda dva , definisanih u odnosu na sredista naspramnih
ivica;
8 osnih simetrija reda tri, definisanih u oba smera u odnosu na prave
odredjene naspramnim temenima. Racunajuci i koincidenciju, kocka raspolaze
sa ukupno 24 rotacije.
Indirektne transformacije su: 6 ravanskih refleksija definisanih u oba
smera u odnosu na bisektralne ravni unutrasnjih diedara; 3 ravanske refleksije
zadate medijalnim ravnima ivica. Od rotacionih refleksija pravilan heksaedar
ima sve tri moguce vrste i to:
6 rotacionih refleksija reda cetiri definisanih u oba smera u odnosu na
prave odredjene sredistima naspramnih pljosni;
8 rotacionih simetrija reda sest definisanih u oba smera u odnosu na prace
odredjene naspramnim temenima i centralnom refleksijom.

Slika: Heksaedar (Euklidovi elementi)
PRAVILAN OKTAEDAR
Pravilan oktaedar ima 48 simetrija
od kojih jedna polovina menja, a druga polvina ne menja njegovu orijentaciju.
To su sledece transformacije:
8 osnih simetrija reda tri, definisanih u oba smera u odnosu na prave
odredjene sredistima naspramnih pljosni;
6 osnih simetrija reda dva , definisanih u odnosu na prave odredjene sredistima
naspramnih ivica;
6 osnih simetrija reda cetiri definisanih u oba smera u odnosu na prave
odredjene naspramnim temenima, kao i tri osne simetrije reda dva definisane
u odnosu na iste prave. Uz koincidenciju, to su sve direktne izometrijske
trnsformacije kojima oktaedar raspolaze.

Indirektne trnsformacije su: 3 ravanske refleksije definisane bisektralnim
uglovima; 6 ravanskih refleksija definisanih medijalnim ravnima ivica;
8 rotacionih simetrija reda sest, definisanih u oba smera u odnosu na
prave odredjene sredistima naspramnih pljosni; 6 rotacionih simetrija
reda cetiri definisanih u oba smera u odnosu na prave odredjene naspramnim
temenima.
Oktaedar raspolaze I centralnom simetrijom.
PRAVILAN DODEKAEDAR
Pravilan dodekaedar ima 120 simetrija. Polvina od njih su direktne izometrijske
transformacije I to:
12 osnih simetrija reda pet, definisanih u oba smera u odnosu na prave
odredjene sredistima naspramnih pljosni;
12 osnih simetrija reda 5/2 definisanih u oba smera u odnosu na prave
odredjene sredistima naspramnih ivica;
20 osnih simetrija reda tri, definisanih u oba smera u odnosu na prave
odredjene naspramnim temenima i naravno koincidencijom.

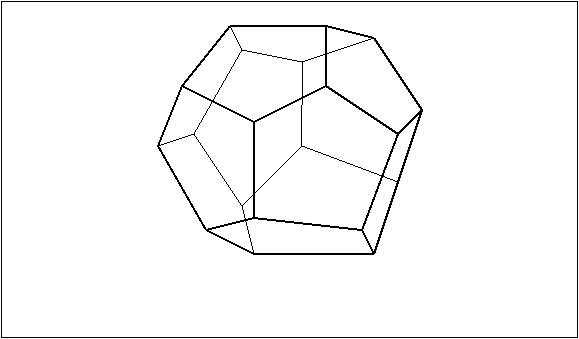
Pravilan dodekaedar raspolaze sa 60 indirektnih transformacija i to:
15 ravanskih refleksija definisanih bisektralnim ravnima unutrasnjih diedara
dodekaedra;
12 rotacionih refleksija reda deset, definisanih u oba smera u odnosu
na prave odredjene sredistima naspramnih pljosni;
20 rotacionih simetrija reda sest, definisanih u oba smera u odnosu na
prave ,tj ravni odredjene naspramnim temenima.
Pravilan dodekaedar raspolaze i centralnom simetrijom.
PRAVILAN IKOSAEDAR
Pravilan ikosaedar ima 120 simetrija od kojih jedna polovina menja njegovu
orijentaciju, a druga ne. To su sledece simetrije:
20 simetrija reda tri , definisanih u oba smera u odnosu na prave odredjene
sredistima naspramnih pljosni;
15 osnih simetrija reda dva , definisanih sredistima naspramnih ivica;
12 osnih simetrija reda 5/2 (u oba smera), u odnosu na prave odredjene
naspramnim temenima i naravno identicno preslikavanje.
Indirektne
transformacije su:
15 ravanskih simetrija definisanih bisektralnim ravnima unutrasnjih diedara;
20 rotacionih refleksija reda tri definisanih u oba smera u odnosu na
prave odredjene sredistima naspramnih pljosni;
12 rotacionih simetrija reda pet, definisanih u oba smera u odnosu na
prave odredjene naspramnim temenima;
12 rotacionih simetrija reda 5/2, definisanih u oba smera u odnosu na
prave odredjene naspramnim temenima.
Pravilan ikosaedar raspolaze i centralnom simetrijom.
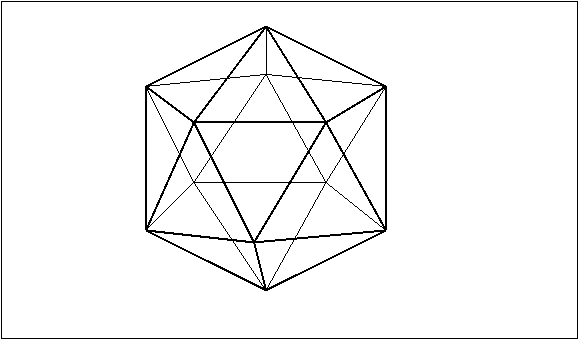

Svaki pravilan poliedar ima istu grupu simetrija kao njegov dualni poliedar, jer rotacije koje ciklicno permutuju temena neke pljosni jednog od ovih dvaju poliedara, istovremeno ciklicno permutuju pljosni oko jednog temena njemu dualnog poliedra.
Literatura:
1. Ljiljana S. Jovasevic Magistarski rad:Grupe simetrija ravanskih i prostornih likova sa primenama u srednjoskolskoj nastavi matematike.
2. Euklidovi elementi
3. Wikipedia, slobodna enciklopedija www.wikipedia.com
4. Z. Lucic : Ogledi iz istorije anticke geometrije
5. H.S.M. COXETER Regular Polytopes
preuzmi
seminarski rad u wordu » » »


