OSTALI SEMINARSKI RADOVI
IZ MATEMATIKE: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
IRACIONALAN BROJ
U matematici, iracionalan broj je onaj realan broj koji nije racionalan broj, tj ne može biti napisan kao razlomak dva cela broja odnosno nije oblikaKratka istorija teorije iracionalnih brojeva
Otkriće iracionalnih brojeva se vezuje za pitagorejce, konkretno za Hipasusa
iz Metapontuma, koji je izveo (najverovatnije geometrijski) dokaz o iracionalnosti
(nesamerljivosti) kvadratnog korena iz broja 2. Prema priči je Hipasus
pokušao da dokaže da je hipotenuza jednakokrakog pravouglog trougla samerljiva
sa katetom, odnosno današnjim rečnikom da je koren iz 2 moguće predstaviti
razlomkom. Usred traženja takvog dokaza on je dokazao upravo suprotno.
Pitagorejska sekta je među svojim dogmama imala da je svet u suštini matematički
i da se sve u njemu može predstaviti odnosom brojeva. Brojevi koji se
nisu mogli predstaviti tako su po njima bili van uma (lat. ratio)
odnosno van pameti, pa ih je neko tako i nazvao, iracionalni (grčki alogon,
što doduše može značiti i ono o čemu ne treba pričati). Hipasus
je, izgleda, nekom van bratstva ispričao o svom otkriću. Pobesnela braća
su ga uljudno pozvala na krstarenje i na pučini bacili preko palube.
U šesnaestom veku je konačno došlo do prihvatanja pojmova negativni brojevi,
celobrojni i razlomljeni deo broja. U sedamnaestom stoleću je konačno
prihvaćen decimalni brojni sistem u današnjem obliku od šire matematičke
zajednice. Abraham de Moavr i Leonard Ojler, u sledećem stoleću, otkrivaju
izuzetno upotrebljive osobine imaginarnog broja. U devetnaestom stoleću
je kompletirana teorija kompleksnih brojeva, iracionalni brojevi su razdvojeni
na algebarske i transcendentne, dokazano je postojanje transcendentnih
brojeva i napravljen novi pristup u oblasti koja je nedirnuta od doba
Euklida, teoriji iracionalnih brojeva. Godine 1872. su svoje teorije objavili
Karl Vajerštras, Čarls Dedekind i Edvarda Hajne. Vajerštrasove i Dedekindove
ideje dalje razrađuju Pinkerle i Taneri. Vajerštras, Kantor i Hajne su
svoj rad zasnovali na redovima dok je Dedekind ideju našao u preseku ose
realnih brojeva razdvajajući sve racionalne brojeve u dve grupe određenih
osobina. Ova tema se dalje razrađuje kroz radove Vajerštrasa, Kronekera
i Mireja.
Leonard Ojler je posvetio pažnju verižnim razlomcima, blisko povezanim
sa iracionalnim brojevima, ali se tek u devetnaestom veku detaljno razrađuju
u delima Žozef Luj Lagranža.
Kroneker je prvi razdvojio transcendentne brojeve od algebarskih. Lamber
je 1761 dokazao da π nije racionalan broj. Dokazao je još da en
nije racionalan ako je n racionalan (osim za n=0). Ležandr
je 1794. godine dovršio Lamberov dokaz i još dokazao da π ne može biti
kvadratni koren racionalnog broja. Žozef Liuvil je 1840. godine pokazao
da ni e ni e2 ne mogu biti rešenja kvadratne jednačine
sa celobrojnim koeficijentima. Postojanje transendentnih brojeva je dokazao
Liuvil 1844. godine ali je tek 1873. pokazan jedan takav. Čarls Hermit
je tada dokazao da je e transendentan a Lindeman je 1882. godine
to isto dokazao za π polazeći od Hermitovih zaključaka. Lindemanov dokaz
je pojednostavio Vajerštras 1885. godine i Dejvid Hilbert 1893. godine
a kasnije su se time bavili i Hurvic i Pol Albert Gordon.
Iracionalnost kvadratnog korena iz 2
Jedan dokaz iracionalnosti kvadratnog korena iz 2 se dokazuje dovođenjem u kontradikciju (reductio ad absurdum), omiljenom metodom starih Helena. Tvrdnja se dokazuje uvođenjem suprotne pretpostavke u odnosu na željenu i kroz dokazni postupak dolazimo do kontradikcije takvoj pretpostavci, što je eliminiše. Tako je naša željena pretpostavka ostala jedina moguća te je stoga tačna.
- Pretpostavimo da je
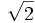 racionalan broj. To znači da postoje prirodni brojevi a i b takvi da je
racionalan broj. To znači da postoje prirodni brojevi a i b takvi da je 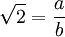
- Tada
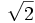 može biti napisan kao neskrativi razlomak
može biti napisan kao neskrativi razlomak 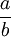 , što znači da su brojevi a i b uzajamno prosti prirodni brojevi i istovremeno
, što znači da su brojevi a i b uzajamno prosti prirodni brojevi i istovremeno 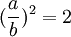 .
. - Sledi da je
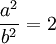 odakle je
odakle je 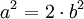 .
. - Odavde je jasno a2 paran broj, jer je predstavljen kao proizvod broja 2 i prirodnog broja.
- Iz ovoga sledi da a mora biti paran, jer je kvadrat parnog broja paran a neparnog broja neparan.
- Pošto je a paran, postoji takvo k da važi
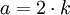 .
. - Kad ubacimo poslednju jednakost u (3) dobijamo: (2k)2 = 2b2, što vodi do 4k2 = 2b2 odnosno posle skraćivanja sa 2 dobijamo 2k2 = b2.
- Iz ovoga sledi da je b2 paran broj jer je predstavljen kao proizvod dvojke i prirodnog broja. Potom iz ovoga sledi da je i b paran jer samo parni brojevi imaju parne kvadrate.
- Iz (5) i (8) sledi da su i a i b parni, što je u direktnoj suprotnosti sa pretpostavkom u (2) da su brojevi a i b uzajamno prosti.
Tako smo dokazali željeno, prvo pobijajući tu tvrdnju a potom dokazujući da nas to dovodi do apsurda i kontradikcije. Zaključak je, ne treba negirati početnu tvrdnju jer je ona tačna. Dakle ![]() je iracionalan.
je iracionalan.
Ovaj dokaz može biti uopšten, da dokaže da je bilo koji koren bilo kog prirodnog broja ili prirodan broj ili iracionalan.
Drugačiji dokaz:
Primenom iste metode na drugačiji način možemo dokazatiSa slike je jasno da su veliki i mali pravougli trouglovi slični. Ako je odnos hipotenuze i katete kod velikog jednak m/n, gde su m i n uzajamno prosti, tada isti takav odnos postoji i kod manjeg i iznosi (2n-m)/(m-n). Ali pošto smo dobili odnos u kome su brojevi u razlomku manji nego u prvom razlomku zaključak je da smo upravo skratili imenilac i brojilac, što je u suprotnosti sa polaznom pretpostavkom da su m i n uzajamno prosti.
Ovo je dokaz u kome nema računa već isključivo geometrije, pa se može smatrati prihvatljivim starim helenskim geometrima
Iracionalnost zlatnog preseka
Kada se duž podeli na dva dela na način da se duži deo prema celini odnosi
na isti način kao kraći deo prema dužem, tada smo duž podelili u zlatnom
odnosu. Kaže se još da smo napravili zlatan presek, čiji je odnos
![]()
Pretpostavimo da je ovaj broj racionalan, i predstavimo ga odnosom n/m gde su n i m uzajamno prosti. Neka je n dužina celine, a m dužina dužeg dela. Tada je dužina kraćeg dela n − m. Sledi da je tada
![]() .
.
Ali ovo znači da smo pojednostavili razlomak koji, prema pretpostavci, nije mogao biti pojednostavljen, skraćen. To je kontradikcija, znači pretpostavka da je φ racionalan nije tačna.
Transcendentni i algebarski iracionalni brojevi
Skoro svi iracionalni brojevi su transcendentni a istovremeno su svi transcendentni brojevi iracionalni. Poznati su sledeći primeri
- er je iracionalno, ako je r ≠ 0 racionalno;
- πr je iracionalno, ako je r ≠ 0 racionalno;
- eπ je takođe iracionalno.
Drugi način konstrukcije iracionalnog broja je iracionalni algebarski
broj tj. kao nula polinoma sa celobrojnim koeficijentima. Pođimo od jednačine
p(x) = an xn + an-1 xn−1
+ ... + a1 x + a0 = 0
gde su koeficijenti ai celi brojevi. Pretpostavimo da postoji
realan broj x takav da je p(x) = 0
Jedini mogući racionalni koren ovog polinoma je oblika r/s
gde je r delilac a0 i s je delilac an.
Postoji konačan broj kandidata i svi se mogu proveriti pojedinačno. Ako
nijedan od njih nije koren p, tada x mora biti iracionalno.
Ova tehnika može biti korišćena da se pokaže da je x = (21/2
+ 1)1/3 iracionalan, jer tada je (x3 − 1)2 = 2 odnosno x6
− 2x3 − 1 = 0, a ovaj polinom nema racionalne korene (jedini
kandidati su ±1).
Zato što algebarski brojevi čine polje, mnogi iracionalni brojevi mogu
biti konstruisani kombinovanjem transcendentnih i algebarskih brojeva.
Na primer 3π+2, π + √2 i e√3 su iracionalni (i transcendentni).
Jednostavan dokaz iracionalnosti za neke logaritme
Logaritmi su verovatno najjednostavniji za dokazivanje iracionalnosti. Sledi dokaz svođenjem na kontradikciju, da je log23 iracionalan:
Pretpostavimo da je log23 racionalan. Znači postoje prirodni brojevi m and n, takvi da je log23 = m/n.
Tada je 2m/n = 3.
Odatle sledi 2m = 3n.
Ali 2 na neki prirodan broj je uvek parno, a 3 na neki prirodan broj je uvek neparno. Sledi početna pretpostavka je pogrešna.
Slučajevi kao što je log102 se dokazuju slično.
Iracionalni brojevi i decimalni razvoj
Često se pogrešno zaključuje da matematičari definišu iracionalan
broj u smislu decimalnog razvoja, nazivajući broj iracionalnim
ako decimalni razvoj ima beskonačno cifara, a cifre se ne ponavljaju.
Nijedan matematičar ne uzima ovo kao definiciju jer izbor osnove 10 za
brojni sistem je prozvoljan a prava definicija je bolja i jednostavnija.
Mada, istini za volju, tačno je da je broj oblika n/m,
gde su n i m prirodni brojevi, ako i samo ako decimalni
prikaz ima konačan broj cifara ili se cifre ponavljaju beskonačno u grupama.
Ovo je moguće pokazati običnim školskim deljenjem n sa m
jer samo m mogućih ostataka postoji. Ako je 0 ostatak, decimalni
ispis se završava. Ako se 0 nikad ne pojavljuje tada se postupak može
ponoviti najviše m − 1 puta pre nego što se ponovo isti ostaci
pojave. Posle toga, ostatak se ponavlja i decimalne cifre se ponavljaju.
Primer:
![]()
Pošto je dužina ponavljajuće grupe cifara 3, pomnožimo sa 103:
![]()
i oduzmimo A od obe strane:
![]()
Tada
![]()
(Broj 135, iz gornjeg primera, se lako nalazi upotrebom Euklidovog algoritma.)
Skup iracionalnih brojeva nema standardnu oznaku kao što je to slučaj
sa skupom prirodnih brojeva N, skupom racionalnih brojeva Q ili skupom
realnih brojeva R.
Skup iracionalnih brojeva je neprebrojiv, dok je skup racionalnih brojeva
prebrojiv a realnih brojeva neprebrojiv. Skup algebarskih iracionalnih
brojeva, znači netranscendentnih, je prebrojiv.
Koristeći apsolutnu vrednost za merenje rastojanja, iracionalni brojevi
čine metrički prostor koji nije kompletan. Pa ipak, ovaj metrički prostor
je homeomorfan kompletnom metričkom prostoru svih nizova prirodnih brojeva.
Primeri:
Neki iracionalni brojevi su algebarski brojevi, kao što
je
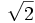 kvadratni koren iz 2,
kvadratni koren iz 2,![\sqrt [3] {5}](pictures/Iracionalan_broj/Iracionalan-broj_clip_image017.gif) kubni koren iz 5
kubni koren iz 5
a neki su transcendentni brojevi, kao što su
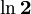 prirodni
logaritam broja 2,
prirodni
logaritam broja 2,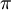 broj
π, Arhimedov broj, Ludolfov broj,
broj
π, Arhimedov broj, Ludolfov broj,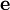 matematička
konstanta e, osnova prirodnog logaritma, Ojlerova konstanta
matematička
konstanta e, osnova prirodnog logaritma, Ojlerova konstanta
Brojevi za koje se ne zna da li su iracionalni :
Ne zna se da li su π + e i π − e iracionalni ili ne.
Ustvari, ne postoje prirodni brojevi m i n za koje se
zna da li je mπ + ne iracionalno ili ne.
Nije poznato ni za ![]() ,
,
![]() ,
,
![]() .
.
preuzmi
seminarski rad u wordu » » »


