OSTALI SEMINARSKI RADOVI
IZ MATEMATIKE: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ЕЛЕМЕНТИ КОМБИНАТОРИКЕ
ВАРИАЦИЈЕ, ПЕРМУТАЦИЈЕ И КОМБИНАЦИЈЕ
При решавању комбинаторних задатака пребројавање готово увек се срећу
основне комбинаторне конфигурације варијације, пермутације и комбинације.
Оне се формирају на одређени начин од елемената неког скупа (на пример,
ређањем елеманата тог скупа у низ, формирањем новог скупа од елемената
датог скупа, . . . )
1. Вариација
Дефинацијa: K-варијација елемената n – скупа А је к-торка
елеманата скупа А, тј. елемант скупа Ак .
Пример 1.1. Нека је А = {a, b}. Запишимо
ове три вариације елемената a и b.
Добијамо
aaa, aab, aba, baa, abb, bab, bba, bbb
*Пример 1:
На тикету спортске прогнозе записано је 13 парова фудбалских екипа, које
ће мођусобно, одиграти утакмицу. Прогнозер крај сваког пара уписује један
од бројева 0, 1 и 2, који редом означавају нерешен резултат, победу домаће
екипе и победу гостујуће екипе. Прогнозирајући све резултате прогнозер
уписује једни 13-вариацију елемената 0, 1 и 2. На основу теореме 1.1 следи
да прогнозер може прогнозирати свих 13 резултата на 313 = 1 594 323 начина.
*Пример 2:
Колико има петоцифрених бројеве у чијем запису нема цифара 6, 7, 8, 9?
Број низова дужине 5 чији чланови припадају скупу {0, 1, 2, 3, 4, 5,}
једнак је 65. Број теквих низова који почињу цифром 0 једнак је 64. Тражени
број једнак је 65 – 64 = 6 480
2. Вариација без понављања
Дефиниција: Претпостављамо да је К ≤ n. Број K – вариација без понављања
елемената n-скупа А је К-торка разлчитих елемената скупа А.
*Пример 1:
Нека је А = {а, b, c, d} запишимо све вариације без понављања елемената
скупа А. Добијамо:
аb, ac, ad, ba, bc, bd, ca, cb, cd, da, db, dc.
Теорема: Нека је К ≤ n. К-вариација без понављања елемената
n-скипа А једнак је n(n - 1). . . (n – k + 1).
Доказ: У К – торки (a1, a2, . . . ,an) различитих елемената n-скупа А,
први члан а1 може бити било који елемент n-скупа А, други члан а2 може
бити било који елемент (n – 1)-скупа А / {a1}, . . . k – ти члан ак може
бити било који елемент (n – k + 1)-скупа A {a1 , a2 , . . . . , ak – 1
}. Према томе, број К – торки различитих елемената n-скупа А једнак је
n(n-1). . . (n-k+1).
*Пример 2: Колико има петоцифрених бројева у чијем запису
нема понављања цифара и нема цифре нула?
Тражени број једнак је 9 ∙ 8 ∙ 7 ∙ 6 ∙ 5 = 15 120
3. Пермутација
Дефиниција: Пемутација n-скупа А је n-вариација без
понављања елемената скупа А.
Јасно је да је пермутација скупа А одређена бијекцијом скупа А на себе.
*Пример 1:
Нека је А = {a, b, c, d}. Запишимо све пермутације скупа А:
abcd, abdc, acbd, acdb, adbc, adcb
bacd, badc, bcad, bcda, bdac, bdca
cabd, cadb, cbad, cbda, cdab, cdba
dabc, dacb, dbac, dbca, dcab, dcba
Број пермутација 4-скупа А једнак је 24.
Теорема: Број пермутација n-скупа А једнак је n!
*Пример 2: Одговоримо на следећа два питања:
(а) На колико начина можемо поређати у низ елементе 1, 2, 3, 4 и 5?
(б) На колико начина можемо поређати у низ елементе 1, 2, 3, 4 и 5, тако
да на прва два места стоје парни бројеви?
КОРИСТЕЋИ ТЕОРЕМУ, ДОБИЈАМО:
(а) 5 датих елемената можемо поређати у низ на 5! = 120 начина.
(б) Бројеве 2 и 4 можемо распоредити на прва два места на 2! начина, а
бројеве 1, 3 и 5 можемо распоредити на остала три места на 3! начина,
па је укупан број распореда једнак 2! 3! = 12.
*Пример 3: На колико начина 8 ученика могу поделити 8
различитих књига, тако да сваки ученик добије једну књигу?
Тражени број једнак је 8! = 8 ∙ 7 ∙ 6 ∙ 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1 = 40 320
4. Комбинација
Дефиниција: Нека је k ≤ n. k-комбинација елемената n-скупа
А је k-подскуп А.
*Пример 1: Нека је А = {a, b, c, d}. 3-комбинације елемената
скупа А су следећи подскупови скупа А: {a, b, c}, {a, b, d}, {a, c, d},
{b, c, d}
Теорема: Број k-комбинација елемената n-скупа А једнак је
Доказ: Нека је Ѕ1 скуп свих k-вариација без понављања елемената n-скупа А, а, Ѕ2 скуп свих k-комбинација елемената скупа А. Из теореме следи да скуп Ѕ1 садржи n(n – 1) . . . (n – k + 1) елемената. Дефинишемо функцију f : Ѕ1 → Ѕ2 на следећи начин: k-вариацији без понављања елемената v = (a1 , a2 , . . . ak) Є Ѕ1 , придружимо k-комбинацију f(v) = s = { a1 , a2 , . . . , ak } Є Ѕ2. Сваки елемент ѕ Є Ѕ2 је слика тачно k! елемената скупа Ѕ1 . На основу теореме добијамо
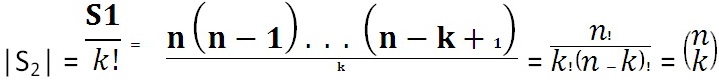

*Пример 3: На колико начина од 10 различитих сувенира
туриста може купити 3 различита сувенира?
Тражи се број 3-комбинације елемената 10-скупа. На основу теореме тај
број је једнак = 120.
*Пример 4: У одељењу има 12 ученица и 8 ученика. Треба изабрати 3 ученице и 2 ученика који ће представљати одељење на такмичењу младих математичара. На колико начина се то може урадити?
Од 12 уценица можемо изабрати њих троје на начина, а од 8 ученика можемо изабрати два на начина. На основу правила производа добијамо да је тражени број једнак = 220 ∙ 28 = 6 160.
5. Варијација датог типа
Дефиниција: Дат је скуп А = {a1 , a2 , . . . . , am}
и на њему строго линеарни поредак а1 < a2 < . . . < am . Нека
су k1 , k2 , . . . , km негативни цели бројеви и
n = k1 + k2 + . . . + km > 0
Тада кажемо: n – варијација елемената скупа А, која има тип (k1 , k2 , . . . , km) је n – торка елемената скупа А, у којој се за сваки број ј Є {1, 2, . . . , m}, елемент ај појављује тачно Кј пута.
*Пример 1: Нека је А = {a, b, c, d} и a < b <
c < d. 5 – варијације елемената скупа А које имају тип (3, 2, 0, 0)
су:
aaabb, aabba, abbaa, bbaaa, aabab,
ababa, babaa, abaab, baaba, baaab.
*Пример 2: Нека је А = {a, b, c, d} и a < b <
c. Свака 3-варијација елемената скупа А има један од следећих 10 типова:
(3, 0, 0), (0, 3, 0), (0, 0, 3), (2, 1, 0), (2, 0, 1),
(1, 2, 0), (1, 0, 2), (0, 1, 2), (0, 2, 1), (1, 1, 1).
Доказ: Због једноставности записа претпоставлјамо да је А = {1, 2, . . .m} Нека је Ѕ скуп свих (n + m – 1) варијација елемената скупа {0, 1, 2, . . . . m} које имају облик
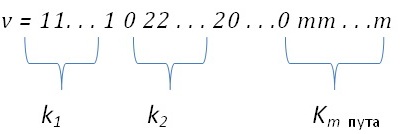
и Т скуп свих типова n – ватиација елемената m – скупа. Свака варијација v Є Ѕ садржи m – 1 нулу и једно значно је одређена положајем нула. Према томе, скуп Ѕ садржи елемената. Функција f : Ѕ → Т, одређена условом f (v) = (k1, k2, . . . , km) је бијекција. На основу тога добијамо
![]()
*Пример 3: Колико има седмоцифрених бројева у чијем
запису се 3 пута појављује цифра 1 и по два пута цифре 2 и 3?
Бројеви са наведеном особином су 7-варијације елемената 1, 2 и 3, које
имају тип (3, 2, 2), па на основу теореме добијамо да је њихов број једнак
= 210
*Пример 4: Колико се различитих речи може добити пермутовањем
слова речи МАТЕМАТИКА?
У запису речи МАТЕМАТИКА три пута се појављује слово А, па два пута слова
М и Т и по једанпут слова Е, К, И. Зато је тражени број једнак
= 151 200
6. Комбинација са понављам
Дефиниција: Нека је на скупу A = {a1, a2, . . . , am}
дат строги линеарни поредак: a1 < a2 < . . . < am. n-комбинација
са понављањем елемената скупа А је n-торка (f(1), f(2), . . . . , f(n)),
која је одређена монотоно растоћом функцијом f : {1, 2, . . . , n} → A,
тј. функцијом за коју важи f (1) ≤ f (2) ≤ . . ≤ f (2)
*Пример: Дат је скуп А = {a, b, c} са линеарним уређењем a < b <
c. Постоји 10 различитих 3-комбинација са понављањем елемената 3-скупа
А и то су
aaa, bbb, ccc, aab, aac, abb, acc, bbc, bcc, abc
Tеорема 1: Број n-комбинација са понављањем елемената m-скупа А једнак је
![]()
Доказ: Нека је скупу А = {a1, a2, . . . , am} дат строги линеарни поредак: a1 < a2 < . . . < am. Нека је К скуп n-комбинација са понављањем елемената m-скупа A и T скуп типова n-варијација елемената скипа А. Дефиношемо функцију f:k →T, која тип (k1, k¬2, . . . ,km) Є K пресликава вариацију
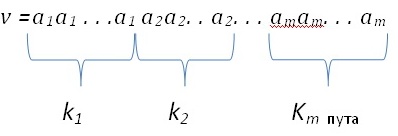
Функција f очигледно је бијекција, па користећи теорему
добијамо
![]()
Tеорема 2: Број n-комбинација са понављањем елемената m-скупа А, у којима
се сваки елемент скупа А појављује бар једанпут, једнак је ![]()
Доказ: Нека је К скуп n-комбинација са понављањем елемената
скупа
А = {a1, a2, . . . am}
У којима се сваки елемент скупа А појављује бар једанпут, а V скуп n-варијација
елемената скупа A U {0}. Дефинишемо функцију f: k→V која n-комбинацију
са понављањем
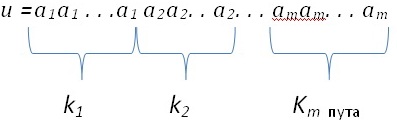
слика у n-вариацију
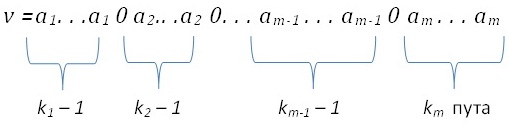
Функција f је очигледно 1 – 1 пресликавање. Нека је
f(K) = {v = f(u)|u Є K}
*Пример 1: На колико начина од 10 врста разгледница
туриста може купити 3 (не обавезно међусобно различите) разгледнице?
Између скупа свих могућих избора 3 разгледнице од 10 врста разгледница
и скупа 3-комбинација са понављањем елемената 10-скупа постоји бијекција,
па на основу теореме 1 добијамо да је тражени број једнак![]() = 180.
= 180.
*Пример 2: Колико има петоцифрених бројева у чијем запису
(гледано слова на десно) цифре чине растући низ?
Између скупа оваквих бројева и скупа 5-комбинација са понављањем елемената
1, 2, 3, 4, 5, 6, 7, 8, 9 постоји бијекција. Зато је тражени број једнак
![]() = 1287
= 1287
ЛИТЕРАТУРА
Комбинаторика Павле Младеновћ
Комбинаторика и графови Слободан Симић
Комбинаторика и графови Драгош Цветковић
preuzmi
seminarski rad u wordu » » »


