OSTALI SEMINARSKI RADOVI
IZ MATEMATIKE: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ISTORIJA MATEMATIKE
MATEMATIKA MESOPOTAMIJE
OSTACI STAROG VAVILONA
Mesopotamija, predručje između i oko Eufrata i Tigrisa, bila je kolevka
jedne od, ili, možda bolje rečeno nekoliko najstarijih kultura. Govoreći
o matematici stare Mesopotamije predrazumijevamo ostavštinu Sumerana,
Babilonaca, Asiraca, Akađana, Kaldejaca i drugih naroda koji su u pojedinim
razdobljima obitavali na delovima tog predručja. Takođe se često izraz
«vavilonski» koristi kao sinonim za ˝mesopotamski˝.
Većina najranijih velikih civilizacija nastala je uz velike reke. One
su omogućile navodnjavanje i time razvoj poljoprivrede, kojom su u dani
uslovi da od života nomada, sakupljača i lovaca pređe na ˝planiranije
gospredarstvo˝ uzgoja bilja, plodova i stoke. Osim toga, velike su reke
redovno u svojim donjim tokovima smirenije, polaganije i dovoljno široke
da bi omogućile i plovidbu te time povezale pojedina pre izolirana naselja
u veće ceone, a to je bio i uslov za stvaranje većih država kao upravnih
ceona. Takve ceone su onda razvijale svoju kulturu i civilizaciju, svaka
na sebi svojstven način, u zavisnosti od okolnosti zavisnim rasnim i drugim
karakteristikama plemena i naroda, prednebljem, prirodnim bogatstvima
predručja itd.
SISTEMI I ZAPISI BROJEVA
Pismo te kulture bilo je primitivno slikovno pismo, ali je ono već vrlo
rano postalo veoma stilizovano, poprimivši oblik nazvan klinasto pismo,
zbog običaja urezivanja znakova pomoću klinu sličnog pisaćeg pribora u
pločice od meke gline koje su kasnije pečene na suncu. Sredinom 19. stoljeća
˝dešifrirano˝ je klinasto pismo. Nađeni se tekstovi relativno lako čitaju,
a klinasto je pismo nekad bilo ˝standardno˝ od vavilonado Persije.
Vavilonci su za predočavanje brojeva koristili heksagezimalni
brojevni sistem – sistem s bazom šezdeset. To je bio prvi sistem
u kojem je jedan te isti znak, mogao označavati različite brojeve već
prema mestu, odnosno prema poziciji koju zauzima.Vavilonci nisu imali
šezdeset različitih znakova za brojeve od nule do 59, već su svaki takav
broj ispisali sa samo dve vrste znakova: po jedan vertikalni, uski omasinu
klina za svaku jedinicu i po jedan tupi omasinu klina za svaku deseticu,
drugim rečima, pojedine znakove heksagezimalnog sistema su ispisivali
aditivno u dekadnom sistemu.
Vavilonci taj nedostatak donekle ublažili time što bi između skupine omasinua
što su predočavale ˝znakove˝ između kojih je trebala biti nula ostavili
veći razmak.
S priličnom se sigurnošću može utvrditi da je glavni, iako ne i jedini,
razlog što su Vavilonci prihvatili heksagezimalni sistem bio u njihovim
vrlo razvijenim astronomskim motrenjima. Vavilonski kalendar je još u
drugoj polovini 3. veka pre n. e. delio godinu na dvanaest meseci po trideset
dana, tj. računao s godinom od 360 dana (što je šest puta šezdeset); potrebne
korekcije uvodile su se uklapanjem trinaestog meseca u (njihovim) ˝prestupnim˝
godinama. Upoređujući to s našim kalendarom s mesecima promenjive duzine
i svakom četvrtom prestupnom godinom, možemo se zapitati koji je kalendar
bolji.
KAKO SU RAČUNALI?
 Naši
izvori informacija koji se odnose na nivo mesopotamijske matematike vrlo
su obimni. Mnogo stotina tablica u klinastom pismu bavi se problemima
što bismo ih danas zvali algebarskim ili se bave geometrijskim odnosima.
Nađeno je mnogo stotina tablica koje služe za računanje. Vavilonci su
se služili tablicama kao što se mi danas služimo npr. logaritamskim
tablicama. Među tablicama množenja bile su i tablice koje bismo mogli
zvati ˝tablicama recipročnih vrednosti˝ pomoću kojih su Vavilonci deljenje
mogli svoditi na množenje. Osim tih tablica, imali su i tablice za kvadrat
i kub te za drugi i treći koren. Nađene su i njihove tablice za vrednosti
od n3+n2 u rasponu od n = 1 do n = 30, kojima su na primer, mogli rešavati
kubne jednacine oblika n3+n2 = a za zadano, poznato a i nepoznato n. .
Naši
izvori informacija koji se odnose na nivo mesopotamijske matematike vrlo
su obimni. Mnogo stotina tablica u klinastom pismu bavi se problemima
što bismo ih danas zvali algebarskim ili se bave geometrijskim odnosima.
Nađeno je mnogo stotina tablica koje služe za računanje. Vavilonci su
se služili tablicama kao što se mi danas služimo npr. logaritamskim
tablicama. Među tablicama množenja bile su i tablice koje bismo mogli
zvati ˝tablicama recipročnih vrednosti˝ pomoću kojih su Vavilonci deljenje
mogli svoditi na množenje. Osim tih tablica, imali su i tablice za kvadrat
i kub te za drugi i treći koren. Nađene su i njihove tablice za vrednosti
od n3+n2 u rasponu od n = 1 do n = 30, kojima su na primer, mogli rešavati
kubne jednacine oblika n3+n2 = a za zadano, poznato a i nepoznato n. .
ARITMETIKA I GEOMETRIJA
Mnogo stotina tablica u klinastom pismu bavi se problemima što bismo ih
danas zvali algebarskim ili se bave geometrijskim odnosima. Po svemu tome
vidimo da je vavilonska aritmetika bila, relativno mereno, vrlo visoko
razvijena. Naravno, pojedini njihovi računi koji bi, s obzirom na to da
rade s ˝konkretnim˝ brojevima, po našoj uobičajenoj klasifikaciji spadali
u aritmetiku, zapravo su po svome duhu, po načinu kako su formirani i
vođeni, jasni dokazi da je tu reč i o algebarskom mišljenju. Na primer,
jedna suma kvadrata prvih deset brojeva pokazuje da su Vavilonci znali
kako treba postupiti da bi se dobio zbir kvadrata koliko god prirodnih
brojeva, počevši od jedan redom dalje.
MATEMATIKA STAROG EGIPTA
 Jedna
od najranijih kultura i civilizacija što ih je čovek stvorio na Zemlji
bila je staroegipatska. I danas ćemo se još uvek ponovno i ponovno zadiviti
pred ostacima te velike baštine, razasutim po muzejima sveta i u svojoj
postojbini: bilo da je reč o umetničkim delima u muzeju u Kairu, npr.
iz zbirke nađene u Tutankamonovoj grobnici, bilo da motrimo ostatke čudesne
građevine kraljice Hatšepsut, njen hram u Der el Bahariju, ili velike
piramide, hram u Luksoru ili grobnica u Dolini kraljeva, bilo da čitamo
šifrirane tekstove iz staroegipatske Knjige mrtvih, bilo da iz sačuvanih
skica i opisa pokušamo rekonstruiseti kako su predizane njihove monumentalne
građevine… U svakom ćemo slučaju ostati iznenađeni pred snagom duha i
volje i pred dubinom misli što su nikle i razvile se u dolini Nila pre
nekoliko hiljada godina.
Jedna
od najranijih kultura i civilizacija što ih je čovek stvorio na Zemlji
bila je staroegipatska. I danas ćemo se još uvek ponovno i ponovno zadiviti
pred ostacima te velike baštine, razasutim po muzejima sveta i u svojoj
postojbini: bilo da je reč o umetničkim delima u muzeju u Kairu, npr.
iz zbirke nađene u Tutankamonovoj grobnici, bilo da motrimo ostatke čudesne
građevine kraljice Hatšepsut, njen hram u Der el Bahariju, ili velike
piramide, hram u Luksoru ili grobnica u Dolini kraljeva, bilo da čitamo
šifrirane tekstove iz staroegipatske Knjige mrtvih, bilo da iz sačuvanih
skica i opisa pokušamo rekonstruiseti kako su predizane njihove monumentalne
građevine… U svakom ćemo slučaju ostati iznenađeni pred snagom duha i
volje i pred dubinom misli što su nikle i razvile se u dolini Nila pre
nekoliko hiljada godina.
I staroegipatska je matematika jedna od najranijih epoha razvoja te nauke.
Posebno jedna od prvih grana matematike, geometrija, već samim svojim
nazivom otkriva i svoje predrijetlo. To je po postanku grčka reč koja
bi, doslovno prevedena, značila "merenje zemlje". A upravo kao
merenje zemlje geometrija se široko razvila već u starom Egiptu. Poslovična
izreka, "Egipat je dar Nila", dovoljno je poznata. Bez blatnjavih
žutih voda te reke što su hiljadama godina natapale zemlju, ne bi se razvila
tako bogata civilizacija starog Egipta. No, posle redovnih velikih poplava
Nila, svake bi se godine granice zemljišnih poseda izbrisale i trebalo
ih je ponovno odrediti – valjalo je, dakle, premeravati zemljišta. Izgradnja
veličanstvenih hramova, piramida, kipova, takođe je zahtevala određena
otkrica iz geometrije.
PAPIRUS
 O
staroegipatskoj matematici doznajemo ponajviše iz dveju glasovitih papirusa:
Ahmesovog ili Rhindovog (levo) i Moskovskog (desno dolje). Rhindov papirus
je 1858. otkrio škotski egiptolog Henry Rhind u Luxoru. To je zapravo
svitak duljine 6 m, širine 30 cm. Pisao ga je pisar Ahmes oko 1650 g.
pr. Kr. i verovatno je nastao tako što je Ahmes prepisivao neki spis star
200 godina. Danas se čuva u British Museumu u Londonu, a sadrži 87 matematičkih
problema.
O
staroegipatskoj matematici doznajemo ponajviše iz dveju glasovitih papirusa:
Ahmesovog ili Rhindovog (levo) i Moskovskog (desno dolje). Rhindov papirus
je 1858. otkrio škotski egiptolog Henry Rhind u Luxoru. To je zapravo
svitak duljine 6 m, širine 30 cm. Pisao ga je pisar Ahmes oko 1650 g.
pr. Kr. i verovatno je nastao tako što je Ahmes prepisivao neki spis star
200 godina. Danas se čuva u British Museumu u Londonu, a sadrži 87 matematičkih
problema.
To je jedna kompletna "studijea o svim stvarima, pogled u unutrašnjost
svega što postoji, saotkrice o tamnim tajnama", kako piše u samom
papirusu. Ahmesov papirus je zbirka tablica i vežbi, retorička u svojoj
formi, koja je namenjena uglavnom učenju matematike. Sadrži vježbe iz
aritmetike, algebre, geometrije i raznih merenja. Moskovski papirus otkrio
je 1893. godine V. S. Golenichev. Dug je 6 m, širok 8 cm. Sadrži 25 problema,
od kojih mnogi nisu čitljivi. Čuva se u Moskovskom muzeju.
KAKO SU RAČUNALI STARI EGIPĆANI?
Stari Egipćani imali su razvijeni
decimalni sistem i svoje oznake za brojeve:
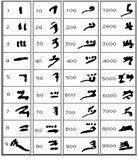 Hijeroglifskim
znacima se pisalo po kamenu kako s leva na desno, tako i obrnuto, a ponekad
i odozgor prema dolje. Različito pisanje ne stvara probleme kod čitanja
bojeva jer egipatski način pisanja brojeva nije pozicijski. Hijeratički
su znaci uvedeni za brzo pisanje po papirusu, drvu ili po lončariji.
Hijeroglifskim
znacima se pisalo po kamenu kako s leva na desno, tako i obrnuto, a ponekad
i odozgor prema dolje. Različito pisanje ne stvara probleme kod čitanja
bojeva jer egipatski način pisanja brojeva nije pozicijski. Hijeratički
su znaci uvedeni za brzo pisanje po papirusu, drvu ili po lončariji.
Osim navedenih, upotrebljavali su se povremeno i neki posebni znakovi
za brojeve koji nisu dekadne jedinice. Npr. za broj dva crtali bi se goveđi
rogovi, za broj pet morska zvezda, a ljudska glava bila je i oznaka za
broj sedam (7 otvora).
Evo nekoliko primera zapisa nekih brojeva:
Koristili su brojevni sistem s bazom 10, a jedna od glavnih razlika između
hijeratičkih brojeva i našeg brojevnog sistema jeste da hijeratički brojevi nisu bili
pisani u sistemu mesnih vrednosti, tako da su poznate mogle biti pisane
bilo kojim redosledom. Hijeratički je sistem adicijski sistem. Vidimo
da se, recimo, broj 249 zapisuje kao 249 = 2 100 + 4 10 + 9, pa u zapisu
imaju dva znaka za 100, četiri znaka za 10 i devet znakova za 1.
brojeva i našeg brojevnog sistema jeste da hijeratički brojevi nisu bili
pisani u sistemu mesnih vrednosti, tako da su poznate mogle biti pisane
bilo kojim redosledom. Hijeratički je sistem adicijski sistem. Vidimo
da se, recimo, broj 249 zapisuje kao 249 = 2 100 + 4 10 + 9, pa u zapisu
imaju dva znaka za 100, četiri znaka za 10 i devet znakova za 1.
Egipatski brojevni sistem nije bio pogodan za računanje, ali je trgovina
zahtevala sabiranje, oduzimanje, množenje, deljenje te rad s razlomcima.
SABIRANJE I ODUZIMANJE
SABIRANJE
Sabiralo se skupljanjem istih simbola zajedno i pretvaranjem njih 10 u
jedan simbol :

ODUZIMANJE
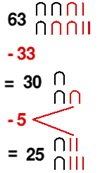 Oduzimalo
se tako da se odmicao određeni broj istih simbola. Ovo je znalo biti i
komplicirano kad se moralo oduzeti više simbola nego što ih je bilo prisutno
u prikazu.
Oduzimalo
se tako da se odmicao određeni broj istih simbola. Ovo je znalo biti i
komplicirano kad se moralo oduzeti više simbola nego što ih je bilo prisutno
u prikazu.
Npr., evo kako bi izračunali 63-38.
Od 6 desetica možemo oduzeti 3 desetice, ali možemo ukloniti samo 3 jedinice.
Još nam preostaje 5 jedinica za oduzimanje.
Jedna od preostalih desetica potrebna je da se omogući oduzimanje sledećih
5 jedinica jer :
1 desetica – 5 jedinica = 10 jedinica – 5 jedinica = 5 jedinica.
Tačan mehanizam oduzimanja koji su koristili nije sasvim jasan, iako ova ilustracija pokazuje kojim je redosledom pisar mogao provesti oduzimanje.
MNOŽENJE I DELJENJE
MNOŽENJE
Množenje prirodnih brojeva odaje nam da su se služili i potencijama broja
2. Stari Egipćani množili su dva broja koristeći udvostručavanje brojeva.
Pogledajte sliku.

U plavom pravougaoniku prikazan je njihov zapis, a sivi pravougaonik i račun ispred pravougaonika objašnjava metodu.
Broj su udvostručavali sabirajuci ga samog sa sobom, dakle samo su zapisali brojeve jedan ispred drugoga i pretvorili svakih 10 istih simbola.
Kako nisu imali razvijen pozicijski zapis brojeva, moramo starim Egipćanima priznati veliku spretnost i ekonomičnost u računanju.
DELJENJE
Deljenje u starih Egipćana zahtijevalo je korištenje množenja i vrlo često
upotrebu razlomaka. Pogledajmo prvo primer deljenja kad je rezultat ceo
broj.
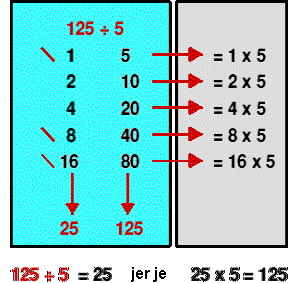
Razmišljanje je sledeće:
• 125 predeljeno s 5 daje isti rezultat kao 5 pomnoženo s ??? = 125
• množi 5 uzastopno s višekratnicima od 2 sve dok ne dobaješ 125 (kao
kod množenja)
• zbir crveno označenih brojeva u plavom pravougaoniku daje rješenje.
Ova metoda temelji se na jednostavnoj matematičkoj činjenici koja je bila
poznata i egipatskim pisarima, a to je da su množenje i deljenje inverzne
operacije, tj.
a∙b = c ako i samo ako je c : b = a.
RAZLOMCI
Na poseban su način označavali razlomke, tako specifičan da nema sličnosti
ni s jednom drugom kulturom. Razlomak s broilacom jedan zapisivao se tako
da se iznad znaka za imenioc stavio poseban znak sa značenjem "deo".
Svi razlomci pisali su se s jediničnim broilacom, a ako to nije bilo moguće,
onda su ga prikazivali kao zbir takvih.
 Kad
je pisar morao računati s razlomcima, bio je suočen s mnogim problemima,
uglavnom vezanim za njihovo zapisivanje. Njihove metode zapisivanja nisu
im dopuštale da pišu jednostavne razlomke kao što su 3/5 ili 15/33 zato
što su svi razlomci morali biti prikazani s broilacom 1. Ako to nije bilo
moguće, onda se razlomak morao zapisati kao zbir razlomaka s broilacom
1. Razlika u tome je bio razlomak 2/3. Razlomci su zapisivani tako da
je iznad imenioca stavljen hijeroglif koji je označavao "otvorena
usta" .Danas pojednostavljeno razlomke s jedinicom u broiocu pišemo
s kosom crtom iza koje slijedi imenioc, npr. 1/2 zapisujemo kao /2, 1/4
kao /4, dok se razlika, 2/3, piše //3.
Kad
je pisar morao računati s razlomcima, bio je suočen s mnogim problemima,
uglavnom vezanim za njihovo zapisivanje. Njihove metode zapisivanja nisu
im dopuštale da pišu jednostavne razlomke kao što su 3/5 ili 15/33 zato
što su svi razlomci morali biti prikazani s broilacom 1. Ako to nije bilo
moguće, onda se razlomak morao zapisati kao zbir razlomaka s broilacom
1. Razlika u tome je bio razlomak 2/3. Razlomci su zapisivani tako da
je iznad imenioca stavljen hijeroglif koji je označavao "otvorena
usta" .Danas pojednostavljeno razlomke s jedinicom u broiocu pišemo
s kosom crtom iza koje slijedi imenioc, npr. 1/2 zapisujemo kao /2, 1/4
kao /4, dok se razlika, 2/3, piše //3.
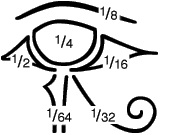
Stari Egipćani verovali su da ih "Rx" simbol, tj. simbol boga
Horusa štiti od zla. Zato su i u matematiku ugradili simboliku pa su razvili
i svojevrstan brojevni sistem koji se koristio za prepisivanje lekova,
predelu zemlje ili sjemenja. Razlomke su tvorili tako što su kombinovali
pojedine delove simbola oka boga Horusa. Svaki deo imao je različitu vrednosti.
Celokupni simbol oka ima vrednosti 1, a ceo sistem se temelji na predeli
na polovice. Pola od 1 je 1/2, pola od 1/2 je 1/4, itd. sve do 1/64.
Npr., da bismo prikazali razlomak 5/8, kombinujemo razlomke 1/8 i 1/2.
GEOMETRIJA
 Posmatramo
li fantastične građevine koje su stari Egipćani ostavili u prilog svetskoj
baštini, ne možemo a da se ne zapitamo koliko su dobro imali razvijenu
geometriju, stereometriju i sve ono što im je bilo potrebno za izgradnju
piramida i hramova. Znamo da su znali računati nagib piramide, obim krnje
piramide te obim piramide. Računali su površinu trougla kao 1/2 mnozenjem
dveju kraćih stranica (što vredi samo za pravouglan trougao); malena odstupanja
nisu im značila previše. Znali su izračunati i površinu pravougaonika
kao proizvod duzina njegovih stranica.
Posmatramo
li fantastične građevine koje su stari Egipćani ostavili u prilog svetskoj
baštini, ne možemo a da se ne zapitamo koliko su dobro imali razvijenu
geometriju, stereometriju i sve ono što im je bilo potrebno za izgradnju
piramida i hramova. Znamo da su znali računati nagib piramide, obim krnje
piramide te obim piramide. Računali su površinu trougla kao 1/2 mnozenjem
dveju kraćih stranica (što vredi samo za pravouglan trougao); malena odstupanja
nisu im značila previše. Znali su izračunati i površinu pravougaonika
kao proizvod duzina njegovih stranica.
Ono što jeste fascinantno, a pronađeno je u Ahmesovom papirusu, je kako
su računali površinu kruga:
• pretpostavimo da krug ima dijametar od 9 kheta (khet je jedinica za
duljinu),
• uzmi 1/9 dijametra, dakle 1,
• ostatak je 8,
• pomnoži 8 sa 8,
• dobaješ 64 i to je površina!
Kad bismo to zapisali savremenim matematičkim jezikom, P = (8/9 x dijametar)2,
i usporedili rezultat s egzaktnom formulom za izračunavanje površine kruga,
, dobali bismo zanimljiv rezultat, stari Egipćani su gotovo 1000 godina
pre stvarnog otkrića broja π znali njegovu približnu vrednovek Naime,
po njihovim računima π bi iznosio približno 3.1605!
Evo i načina na koji se može dobati formula slična egipatskoj za površinu
kruga. Upoređujemo krug s kvadratom:
• precnik kruga je 9, dakle, opiši mu kvadrat stranice duljine 9
• predeli svaku stranicu kvadrata na trećine
• formiraj osmougao kao na slici
• površina dobavenog osmougla približno je jednaka površini kruga
• površina osmougla jednaka je površini kvadrata umanjena za dva mala
kvadrata sačinjena od 4 "odrezana" trougla
ALGEBRA
Staroegipatska algebra bila je retorička, problemi i rešenja dani su
rečima. Znali su rešavati jednacine prvog stepena s tim da su obavezno
provodili analizu i sintezu pri rešavanju, tj. svako rešenje su uvrštavali
u početni problem da se uvere da to uistinu i jeste pravo rešenje.
Stari Egipćani nisu poznavali oznake za množenje, deljenje, jednakost,
drugi koren, decimalnu tačku, nisu čak ni znali za "obični"
razlomak p/q, nisu se pitali zašto nešto funkcionise, nisu tražili univerzalnu
istinu formulisanu simbolima koji bi jasno i logički pokazali njihov misaoni
proces. Ali su se zato koristili i sedmeropoznatastim brojevima, imali
su neku čudnu mešavinu jednostavnosti i čudne komplikovanosti u svojim
računima, ali taj se koncept pokazuje kao potpuno jedinstvena i zatvorena
celina.
Zato se može reći da je egipatska matematika jedini sačuvani čisti primerak
računske tehnike koja je bila vrlo razvijena, koja u čitavom svom razvoju
nije doživela nikakav bitni diskontinuitet, već se u potpunosti temelji
na osnovi računanja - na brojenju i pojmu razlomka.
MATEMATIKA DREVNE KINE
 Obično
kada se govori o matematici Istočne Azije tada se u obzir uzimaju doprinosi
Kine, Koreje i Japana kao jedne velike celine. Matematičari ovih zemalja
smatrani su delom jedne velike zajednice koja je pisala kineskim znakovima
te je kao takva bila izdvojena od drugih civilizacija koje nisu bile upoznate
s tim znakovima. Kina je ostatku sveta postala poznata tek zahvaljujući
Marku Polu, te raznim drugim misionarima (isusovci) koji su putujući svetom
i trgujući došli u kontakt s kineskom civilizacijom i matematikom.
Obično
kada se govori o matematici Istočne Azije tada se u obzir uzimaju doprinosi
Kine, Koreje i Japana kao jedne velike celine. Matematičari ovih zemalja
smatrani su delom jedne velike zajednice koja je pisala kineskim znakovima
te je kao takva bila izdvojena od drugih civilizacija koje nisu bile upoznate
s tim znakovima. Kina je ostatku sveta postala poznata tek zahvaljujući
Marku Polu, te raznim drugim misionarima (isusovci) koji su putujući svetom
i trgujući došli u kontakt s kineskom civilizacijom i matematikom.
Najstariji sačuvani matematički tekstovi potječu tek iz doba oko 200. pre nove ere, no to je posljedica spaljivanja svih knjiga godine 213. pre nove ere po naredbi vladajućeg tiranina.
O Kini se može naći mnogo zanimljivosti, ali možda je važno spomenuti
da je Kina treća zemlja po veličini u svetu te i najmnogoljudnija zemlja
sveta. Kineska kulturna tradicija je jedna od najstarijih u svetu. Pri
tome, ako se gledaju sami začeci kulture na tom predručju, ona nije starija
od nekih drugih kultura npr. sumerskih i egipatskih, ali ono što je naročito
zanimljivo je to da se Kineska kultura neprekidno i kontinuirano razvijala
mnoga vekova, vekova u kojima su razne druge kulture i civilizacije već
odavno nestale. Stoga možemo zaključiti da po kontinuitetu trajanja nema
nijedne druge kulture u svetu koja bi se mogla uporediti s kineskom.
Kineska dostignuća
1. prvi su proizveli papir
2. otkrili su barut
3. proizveli su prvi kompas
4. otkrili su masinu pomoću pomičnih znakova (mnogo pre Gutemberga)
5. seizmograf
6. lančani viseći most . . . itd.
Osim tih ostvarenja, Kinezi su jako poznati i po svom graditeljstvu npr.
˝Zabranjeni grad˝ koji je nekadašnja carska palata dinastije Ming i Ching
je jedan od najvažnijih spomenika arhitekture svih vremena.
Tu je i ˝Veliki kineski zid˝ koji je jedina građevinana Zemlji napravljena
ljudskom rukom, a koja je vidljiva golim okom s Meseca..
POČECI RAZVOJA MATEMATIKE
Ne zna se točno kada se u Kini počela razvijati matematika, ali pretpostavlja
se da je to bilo u 3. veku pre Hrista. Prema starim kronikama ˝Žuti car˝
Huang – Ti (vladao Kinom u 27.veku pre nove ere) dao je naredbe svojim
predanicima tj. zadao im je zadatke šta moraju istraživati. Tako je trima
naucnicima dao zadatak da proriču pomoću Sunca, Meseca i zvezda. Četvrtom
naucniku dao je zadatak da stvori muzicke note, petom naucniku Tai – Naou
naredeo je da konstruise seksagezimalni sistem (Chia – Tsu), šesti naucnik
Li – Skouu dobio je zadatak da izgradi brojeve i umjetnost aritmetike,
a poslednji sedmi naucnik dobio je zadatak da regulise svih tih šest veština
te razradi kalendar.
Koristili su se seksagezimalno – heksagezimanim sistemom. To je najstariji kineski sistem numeracije. Baza mu je broj 60, a funkcioniseo je tako da su se brojevi od jedan do šezdeset tvorili kombinovanjem elemenata jednog desetočlanog i jednog dvanaestočlanog ciklusa. Taj su sistem koristili za brojanje dana i godina.
Naucnici su kasnije ustvrdili da su počeci matematike u Kini imali srodnosti s počecima razvoja matematike u staroj Mezopotamiji i vjeruje se da su ne neki način povezani. Prvi dokazi matematičke aktivnosti u Kini pronađeni su u obliku numeričkih simbola zapisanih na tankim kostima stoke i drugih životinja, a procenjeni su da potiču iz 14.pre nove ere
LEGENDA O LO SHU
 Budući
da nema drugih konkretnih pisanih dokaza, sve se oslanja na jednu legendu
koja govori kako su Kinezi došli na ideju da stvore sistem brojeva i istraživanja
koje je dovelo do razvoja matematike:
Budući
da nema drugih konkretnih pisanih dokaza, sve se oslanja na jednu legendu
koja govori kako su Kinezi došli na ideju da stvore sistem brojeva i istraživanja
koje je dovelo do razvoja matematike:
Prema legendi, kralj Yu je primio dva božanska dara. Prvi dar je primio
od božanske ˝Kornjače˝ dok je prelazio Žutu reku. Na Kornjačinim leđima
je bila zacrtana jedna figura, odnosno, dijagram zvan Lo shu, za koji
se vjeruje da sadrži osnove kineske matematike. Drugi dar, odnosno figuru,
primio je od božanskog konjonogog ˝Zmaja˝ kojem su kopita ostavljala tragove
u blatu.
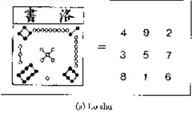
Izrazi li se Lo Shu brojevima (na slici levo – koliko na pojedinom mjesteu
ima u skupinu povezanih točaka) dobava se taj ˝magični kvadrat˝ sa svojstvom
da je zbir brojeva u bilo kojem njegovom retku, stupcu ili po dijagonalama
jednak 15 ( na slici desno).
Taj prvi dijagram, Lo - Shu, kasnije nazvan ˝čarobni kvadrat˝ doveo je
do razvoja dualističke teorije Yina i Yanga, odnosno do dualističkog razvoja
brojeva.
Yang predstavlja neparne brojeve (1, 3, 5, 7, 9, 11...).
Yin predstavlja parne brojeve (2, 4, 6, 8, 10...)
Kasnije su Kinezi uz parne i neparne brojeve usvojili koncept nule. Znak
za nulu je dugo vremena nepoznat. U osmom se veku nula označava tačkom,
a krug ili kvadrat kao simboli za nulu se pojavljuju tek u 13. veku.
KINESKI BROJEVI
U Kini su ljudi, kao i u većini drugih zemalja, najpre računali ˝na prste˝, a već u 2. veku pre nove ere u Kini su imali simbole za brojeve, a oni su prikazani u tablici:

2000.god. pre nove ere
Kasnije se u Kini računalo pomoću štapića (od bambusa, slonove
kosti ili metala). Svi štapići su bili jednake veličine, a trgovci i su
ih najčešće nosili stalno sa sobom u torbi. Brojevi od 1 - 5 bili su prikazivani
kao horizontalne crtice, odnosno kao polegnuti bambusovi štapići, brojevi
od 6 – 9 su prikazivani kao jedan vertikalni štapić te kombinacija od
nekoliko horizontalnih štapića.

400.god pre nove ere
Nakon uvođenja negativnih brojeva, štapići za računanje su se izrađivali
u dve boje - crveni za pozitivne i crni za negativne brojeve.
Mnogo kasnije, tek u 16. stoljeću će se pojaviti abakus. Abakus
je preteča današnjih kalkulatora, a sastojao se od drvenog okvira i niza
žica po kojima su se mogli pomerati kamenčići. On se koristio do usvajanja
arapskih brojeva, a zanimljivo je to da se ponegde u Kini trgovci još
uvek njime služe.
Kineski Abakus
S vremenom kinesko se pismo malo promenilo i oblikovalo. U sledećoj tablici
možemo videti savremene kineske znakove za brojeve. Isti zapis brojeva
može se naći i u Japanu i Koreji.

Savremeni kinesko-japansko-korejski brojevi
Razlomci su se pojavili u upotrebi gotovo istovremeno s prirodnim brojevima.
Osnovne računske operacije izvodile su se slično kao i danas, s tim da
su množenje i deljenje objašnjavali na konkretnim primerima. Dalje se
matematika razvijala iz skupa algoritama za računanje i metoda za rešavanje
praktičnih zadataka.
NAJVAŽNIJA DOSTIGNUĆA
Kao i indijska, kineska matematika nije deduktivnog tipa, nego orjentisana
na nalaženje algoritama za rješavanje konkretnih zadataka. Mnoga od otkrića
i postignuća u matematici Kineza očuvana su u nekoliko starih i veoma
važnih knjiga pisanih u periodu od 1. do 13.vek
Dela:
Knjiga o menama (I Ching) - jedna od najstarijih očuvanih knjiga. Koristila
se za proricanje i gatanje. Sadrži elemente binarne notacije brojeva.
Sveta knjiga o aritmetici (Chou – Pei) - nastajala je u periodu od 2.
– 12. veka. Sadrži predatke, tvrdnje, razgovore i rasprave o matematici,
filozofiji, numerologiji, astronomiji ...U toj knjizi se prvi put spominje
tekst koji na indirektan način govori o Aritmetika u devet knjiga ( Chiu
Chang Suan Shu ) - je najstariji matematički tekvek Njen autor je Chang
Tsang. U toj je knjizi niz od 246 zadataka s rešenjima namenjenih meračima,
inženjerima, činovnicima i trgovcima. U svakoj od knjiga raspravlja se
o jednom matematičkom problemu:
1. daje se postupak izračunavanja površine trougla, četverouglakruga, kružnog odsečka i isečka. Obrađuju se i razlomci; date su korektne metode za njihovo sabiranje, oduzimanje, množenje i deljenje
2. obrađuje se kamatni račun
3. govori o produženim razmerama
4. obrađuje se vađenje drugog i trećeg korena, te približni proračun opsega kruga date površine i precnika kugle datog obima
5. uči se kako se računa obim prizme, piramide, valjka, prikraćene (krnje) piramide
6. obrađuje se ono što bismo zvali računom smese
7. obrađuju se problemi sistema od dveju jednacina sa dve nepoznate
8. ispituju se problemi što vode na sistem od više linearnih jednacina sa vise nepoznatih
9. rešava se pravougaoni trougao pomoću «Pitagorine» teoremae,neke oblike kvadratne jednacine
MATEMATIČARI DREVNE KINE
Zhang Qiu-Jian (5. vek) – razvija ideje prethodnika i
donosi nove matematičke probleme o nizovima brojeva, jednacinama višeg
reda i teoriji brojeva. Dao je formulu za sumu aritmetičkog niza.
Tsu Chung – chih (430 – 201) – za tačnu vrednost broja
π uzima vrednosti , što daje šest tačnih decimalnih mesta (ista vrednosti
u Europi se pojavljuje tek 1600.god, odnosno vek kasnije).
Quin Jiu - Shao (1202 -1261) - rešava sisteme kongruencija,
a posmatra i algebarske jedncine, površine geometrijskih likova i sisteme
linearnih jednacina.Tražio je i rešenja jednadžbi metodom koju nazivamo
Hornerova (William Horner, 1819.), iako je u Kini bila poznata 500 godina
ranije.
Chu Shih - kieh (1270 - 1330.) - napisao je dva važna
teksta: Uvod u matematiku za početnike i Dragoceno ogledalo četiri elementa
(1303.) koje je vrhunac kineske matematike i nakon njega duze vremena
nema napretka u matematici. Sadrži metodu transformacija za rešavanje
jednacina, koju koristi do stepena 14, te ˝Pascalov˝ trougao binomnih
koeficijenata, koji je u Kini poznat četiri veka pre no što ga je Pascal
˝otkrio˝.
STAROINDIJSKA MATEMATIKA
Matematika nije nezavisna od ljudi koji je stvaraju. Staroindijska matematika
bila je pretežno ˝aritmetičko-algebarski˝ orjentisana, za razliku od starogrčke
matematike koja je bila pretežno ˝geometrijski˝ orjentisana. Naravno,
Grčka matematika nije bila isključivo geometrija, niti je staroindijska
matematike bila bez geometrije; reč je samo o usmerenju koje je dominiralo.
U staroindijskoj literaturi nema velikih dela isključivo posvećenih matematici;
matematika je prisutna tek kao deo, kao pojedinačno poglavlje u astronomskim
ili astrološkim delima.
POČECI RAZVOJA MATEMATIKE
Uvođenje posebnih znakova za brojeve od nula do devet u staroindijskom
dekadnom sistemu, donosi bitan napredak staroindijske matematike.
Ti znakovi za brojeve vrlo su slični našima, dakako zbog toga što su naši
znakovi i sami nastali od indijskih uz modifikacije do kojih je došlo
njihovim prenosom što ga Europa zahvaljuje Arapima.
Pozicioni sistem već su ranije koristili Vavilonci i upotrebljavali i
za označavanje razlomka, a ne samo celih brojeva. Stari su Indijci pozicioni
sistem pisanja brojeva upotrebljavali samo za cele brojeve, a ne i za
razlomke.
Otkriće nule kod Indijaca novijeg je datuma nego vavilonsko (nije isključeno
da je možda bilo i pred njegovim uticajem). Kao što je već spomenuto,
bitan napredak staroindijske matematike bilo je uvođenje znakova za brojeve.
Vavilonci takav zapis brojeva nisu imali u svome heksagezimalnom
sistemu, već su brojevi od jedan do pedeset i devet ispisivali
aditivno znacima za deseticu i jedinicu.
Najstariji zapisi koji su nam sačuvani, a sadrže rane oblike indijskih
cifara nalaze se na kamenim stubovima što ih je u svakom značajnom gradu
stare Indije dao predići vladar Maurya-carstva, kralj Asoka, sredinom
3. veka pre nove ere.
Indijsko otkriće nule, ukoliko je uopstenezavisno od vavilonskog, bilo
je usko povezano sa indijskom filozofijom i religijom.
Svakako je znak za nulu Indijcima omogućio spretnije računanje. Više nije
bila potrebna računska ploča sa stupcima ili poljima, gde je prazno polje
značilo ˝ništa˝ i bilo bez posebnog znaka.
KAKO SU RAČUNALI?
Na primeru ćemo ilustrovati kako su stari Indijci na računskim pločama
predijeljenim na polja obavljali množenje,ispisujući i brišući brojeve
na pesku kojim bi posipali ploču.
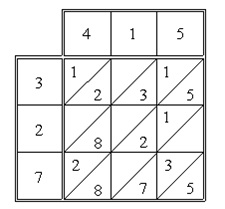
Ako je trebalo, recimo, pomnožiti 415 sa 327 ispisali bi te brojeve u
glavni redak i stub računske ploče. U svako dijagonalom predeljeno polje
ispisali bi zatim parcijalni proizvod odgovarajućih poznatih, npr. u treće
polje prvog reda ispisali bi poznate jedan i pet, jer je pet puta tri
jednako petnaevek Kada su tako sva polja bila ispunjena (znak za nulu
tu nije potreban jer ga može nadomestiti prazno polje).
Sabirali su brojeve po ˝dijagonalnim prugama˝ počevši od donjega desnog
ugla (uz prenos u dalju prugu ulevo eventualnih desetica – kao i pri našem
množenju).
Matematičke zadatke su stari Indijci često zaodevali u pesničko ruho:
“Jedna petina nekog roja pčela spustila se na cvet Kadambe, a jedna trećina
na cvet Silindhe.
Trostruka razlika tih brojeva odletela je do cvetova Uglova. Preostala
je još jedna pčela, lebdeći u vazduhu amo- tamo, podjednako privučena
dražesnim mirisom jasmina i pandama. Reci mi, divna ženo, koliko je pčela
bilo u roju?”
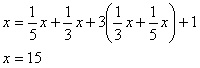
Metoda staroindijskog rešavanja aritmetičko-algebarskih problema često
je bila “inverzija”, u smislu da se traženi broj konačno dobija nizom
postupaka koji se provode redom suprotno predacima što su o njima dani.
Počevši od rezultata prema traženom broju, svaka se operacija zameni suprotnom
(sabiranje sa oduzimanjem, ..).
NAJVAŽNIJA DOSTIGNUĆA
Stari Indijci su imali i vrlo dobre aproksimacije broja ¶.
Zamenjivali su ga sa:
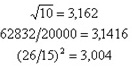
Imali su i odličnu aproksimaciju za broj koren od 2 točnu na pet decimalnih
mesta.
![]()
Takođe, Indijci su vrlo rano znali i za ˝staroegipatski˝ trougao sa stranicama 3, 4, 5, kao u za pravougaoni trougao sa stranicama 15, 36, 39.
STAROINDIJSKI MATEMATIČARI
Najveći i najvažniji staroindijski matematičari:
- Aryabhatta (V vek)
- Brahmagupta (VI. vek)
- Mahavira (IX vek)
- Bhaskara (XII vek)
Aryabhatta, već je među ostalim, znao vaditi drugi i treći koren predelom
radikanda u grupe sa po dve odnosno tri poznate (u načelu isto kao što
radimo danas).
Brahmagupta nalazi celobrojna rešenja nekih kvadratnih jednacina oblika:
![]()
Ovakvo ispitivanje, gde se traže samo celobrojna rešenja neke jednacine
ili nekog sistema jednacina, dobilo je ime po grčkom matematičaru Deofantu,
iako je Indijcima već poznato od ranije. Govori se o ˝deofantskim jednacinama˝,
iako otkrivene od Indijaca.
Stari su Indijci rješavali i ˝deofantsku˝ kvadratnu jednacinu oblika ![]() i to metodom koju je na Zapadu tek u 18. veku ponovno otkrio L. Euler.
i to metodom koju je na Zapadu tek u 18. veku ponovno otkrio L. Euler.
Mahavira se bavio elementarnom matematikom.
Bhaskara dokazuje Pitagorin dokaz iskoricavanjem svojstava sličnosti trougla
(U Europi je ovakav dokaz otkriven tek u XVII. vek)
Nakon Bhaskare indijska je matematika, opste uzevši, stagnirala i čak
nazadovala sve do novijeg vremena. Tek u 20. veku ona se izvanredno razvila
tako da je danas ne samo među prvima u Aziji, već ima svoje mesto i u
svetskim razmerama.
Najveća zvezda novije indijske matematike svakako je bio Srinivasa Ramanujan
(1887-1920). On je naročito za šest poslednjih godina svog kratkog života
što ih je proveo u Engleskoj radeći kod velikog matematičara G. H. Hardya,
dao matematici velike nove priloge trajne vrednosti.
STAROGRČKA MATEMATIKA
 Vrlo
se često tvrdi da je i najstarija grčka nauka samonikla i da nema veze
s vavilonskom i egipatskom civilizacijom. Međutim, između rane grčke nauke
i prvih civilizacija postoji jasna veza. Mnogi starogrčki tekstovi spominju
putovanja grčkih naucnika i filozofa, posebno Talesa
i Pitagore, u te zemlje, ističući da su ti
naucnici tamo upoznali pojedina matematička otkrica. Nisu Grci ponovno
otkrili ona otkrica koja su već bila poznata u Babilonu i Egiptu, oni
su to otkrice preuzeli i interpretirali ih na nov način. Do Grka matematika
je bila pretežno „empirijska“. Stari su Grci bili prvi koji su sebi, svesni
toga što time čine, postavili zadatak da sva predjašnja i sva nova matematička
otkrica skupe i povežu u skladan i celovit sistem unutar kojeg će svaka
teorema i svaka „formula“ biti dokazani. Prešlo se u matematici na apstraktna
razmišljanja i dokaze.
Vrlo
se često tvrdi da je i najstarija grčka nauka samonikla i da nema veze
s vavilonskom i egipatskom civilizacijom. Međutim, između rane grčke nauke
i prvih civilizacija postoji jasna veza. Mnogi starogrčki tekstovi spominju
putovanja grčkih naucnika i filozofa, posebno Talesa
i Pitagore, u te zemlje, ističući da su ti
naucnici tamo upoznali pojedina matematička otkrica. Nisu Grci ponovno
otkrili ona otkrica koja su već bila poznata u Babilonu i Egiptu, oni
su to otkrice preuzeli i interpretirali ih na nov način. Do Grka matematika
je bila pretežno „empirijska“. Stari su Grci bili prvi koji su sebi, svesni
toga što time čine, postavili zadatak da sva predjašnja i sva nova matematička
otkrica skupe i povežu u skladan i celovit sistem unutar kojeg će svaka
teorema i svaka „formula“ biti dokazani. Prešlo se u matematici na apstraktna
razmišljanja i dokaze.
RAZVOJ STAROGRČKE MATEMATIKE
O epohi formiranja grčke matematike možemo da zaključujemo samo na osnovu
manjih fragmenata, koji se nalaze u kasnijim radovima, kao i na osnovu
zapažanja filozofa i drugih autora koji nisu bili samo matematičari.
U vreme pojave prvih zapisa o grčkoj matematici, grčki pomorci i trgovci
su bili već naučili od svojih egipatskih mušterija, da za pisanje upotrebljavaju
papirus, koji se mogao lakše nositi i čuvati nego glinene tablice starih
semitskih civilizacija. U međusobno udaljenim zajednicama istoga jezika,
bogati trgovci i pomorci ovladali su pismenošću, bez uticaja neke moćne
svesteničke kaste. Oni su bili spremni da prilagode korisno znanje, sticano
na putovanjima, paktičnim potrebama.
Period tokom koga su grčke mediteranske zajednice dale trajan doprinos
razvoju matematike može se podeliti u tri velike faze. Prva,
koja nije ostavila nikakvih pisanih tragova, proteže se od Talesa
i Pitagore do Demokrita, približno od 600-400. godine pre n.e. Osnovu
druge faze predstavlja učenje Platona
(430-349. godine pre n.e.). Ona kulminira u Euklidovom
sistemu, koji se veoma oslanjao na Eudoksa (408-355. godine pre n.e.),
Platonovog učenika. Euklidova smrt prethodi za nekoliko godina Arhimedovom
rođenju (oko 287. godine pre n.e.) čija naklonost ka pronalascima
predstavlja početak treće faze. Treću fazu tj. aleksandrijsku
fazu odlikuje odstupanje od formalizama i jak osećaj za praktičnu primenu
matematike.
STAROGRČKI MATEMATIČARI
Grčka tradicija ističe Talesa kao osnivača grčke matematike mada o tome
nema dokumentovanih podataka, ranijih od jednog veka posle Talesove smrti.
Prema podacima drugih autora, on je napisao samo dve rasprave: O solsticiju
i O ekvinociju - jer je mislio da se ostalo ne može saznati. Izgleda da
je, prema nekim autorima, prvi proučavao astrologiju, da je prvi predskazao
Sunčeva pomračenja i utvrdio ravnodnevice. Tako tvrdi Eudem u svojoj Istoriji
astrologije. (Astrologija znači „proučavanje zvezda" i ima u Grka
samo to značenje; dakle, isto što i astronomija.) To je bio razlog divljenja
koje su prema njemu osećali Ksenofan i Herodot. S njime se slažu i Heraklit
i Demokrit.
Tales je poznat po tome što se smatra prvim Helenom koji je izlagao i dokazao teoreme, te stoga i ocem helenske matematike.
Pripisuje mu se sledećih 5 teorema:
1) Prečnik polovi krug.
2) Uglovi na osnovici jednakokrakog trougla su jednaki.
3) Naspramni uglovi koje formiraju dve prave koje se seku su jednaki.
4) Ugao upisan u polukrug je prav.
5) Trougao je određen jednom stranicom i uglovima naleglim na nju.
 U
matematici se više zna i pominje Pitagora,
verovatno zbog toga što je za sobom ostavio školu tzv. pitagorejce koji
su se uprkos i najžešćem proganjanju, održali dugo posle njegove smrti.
Smatra se da je Pitagora, kao i Tales svoje znanje doneo u mnogome iz
Egipta.
U
matematici se više zna i pominje Pitagora,
verovatno zbog toga što je za sobom ostavio školu tzv. pitagorejce koji
su se uprkos i najžešćem proganjanju, održali dugo posle njegove smrti.
Smatra se da je Pitagora, kao i Tales svoje znanje doneo u mnogome iz
Egipta.
Pitagorina teorema je jedna od osnovnih i najznačajnijih matematičkih
teorema. Na osnovu nje je stvoren fraktal koji se naziva pitagorino drvo.

Pitagora za sobom nije ostavio nikakva pisana dela, a za nekoliko spisa koji su u antici kružili pod njegovim imenom utvrđeno je da su nesumnjivo apokrifni. Pitagorino učenje bilo je tajnog karaktera i prenosilo se samo usmeno na neposredne učenike, koji su njegov nauk obično citirali uz izraz ατς φη (lat. ipse dixit = "lično je rekao").
 Razvoj
matematike se sastojao pored nalaženja novih činjenica geometrije i u
koriščenju deduktivne metode u geometriji.To će dati Euklidove elemente.
Euklid je bio Platonov student
u Atini, dok je većinu života proveo radeći u Aleksandriji, u Egipatu,
gde je osnovao matematičku akademiju.
Razvoj
matematike se sastojao pored nalaženja novih činjenica geometrije i u
koriščenju deduktivne metode u geometriji.To će dati Euklidove elemente.
Euklid je bio Platonov student
u Atini, dok je većinu života proveo radeći u Aleksandriji, u Egipatu,
gde je osnovao matematičku akademiju.
Euklid je napisao brojna dela, od kojih neka nisu sačuvana i
poznata su samo po naslovu. Sačuvana su dela: „Elementi“, „Data“, „Optika“
i dr. Negevo najčuvenije delo su "Elementi", koje je uticalo
na zapadno akademsko mišljenje. Smatra se da su nastali oko 325-te godine
pre n.e. dok je Euklid još živeo u Atini. Elementi su podeljeni u trinaest
knjiga; cetiri prve posvecene su geometriji u ravni i bave se proucavanjem
poligonalnih ili kruznih figura. Tu je najpre definicija tacke, “ono sto
nema delova”; zatim linije – “duzina bez sirine”; povrsi – “ima samo duzinu
i sirinu”; prava linija je “jednako postavljena izmedju tacaka” i ravan
je “jednako postavljena izmedju svojih pravih”.
Arhimed iz Sirakuze, smatra
se jednim od trojice najgenijalnijih matematičara svih vremena, bio je
vrhunac helenske matematike i najveći fizičar starog veka.
Heureka! Heureka!(grč. prefiks glagola heursiko - nađem, izračunam, izmislim)
Našao sam, uzviknuo je Arhimed kada je, sedeći u kupatilu, otkrio fizički
zakon da svako telo, potopljeno u tečnost, gubi od svoje težine onoliko
kolika je težina njime istisnute tečnosti ( ili gasa ). Taj gubitak je
u stvari potisak tečnosti ili gasa.
Najpoznatija dela su: O kvadraturi parabole, O lopti i valjku, O računu
sa peščanim zrncima, O ravnoteži ravnih likova, O merenju kruga, O plivanju
tijela, O konoidima i sferoidima.
U ratu sa Rimljanima 47. godine pre n.e. izgorela je Aleksandrijska
biblioteka. Godine 342. uništena je i druga biblioteka u naletu rulje
koja je bila fanatizovana od hrišćanskog arhiepiskopa. Poslednji matematičari
nestaju iz Aleksandrije u V veku. Time se završava cvetanje nauke u Aleksandriji.Posle
toga je središte naučnog života bila stara Platonova Akademija u Atini.
Već oko 100 godina kasnije, 529. godine, car Justinijan je zabranio, pagansku
nastavu i zatvorito Akademiju.
ARAPSKI DOPRINOS MATEMATICI
Mnogi smatraju da u razdoblju od kraja grčke antičke nauke do kasnog
srednjeg veka u Europi nije bilo važnih događaja u matematici osim prevođenja
grčkih tekstova na arapski koji su tako - ne direktno preko rimskog nasleđa,
već indirektno preko arapskih osvajanja - postali dostupni Europi srednjeg
veka. No, zapravo je doprinos arapskog predručja matematici mnogo veći
od samog prevođenja i prenosa predataka. Današnja matematika zapadnog
stila mnogo je sličnija matematici kakvu susrećemo u arapskim doprinosima,
nego onoj u starogrčkim. Mnoge ideje koje su pripisane Europljanima kasnog
srednjeg veka i renesanse pokazale su se zapravo arapskim. Ovde ćemo opisati
razdoblje od 8. do 15. veka.
Prvi predstavnik nauke i prevođenja grčkih tekstova (npr. Euklidovih Elemenata)
na arapski bio je kalif al-Hajjaj, koji je na vlast stupio 786.g. Glavni
naucni centar postaje Kuća mudrosti, vrsta akademije ili sveučilista u
Bagdadu (koji je osnovan 762.g.), koju je početkom devetog stoljeća osnovao
al-Hajjajev sin kalif al-Ma'mun.
 Prvi
veliki arapski matematičar je Al-Khwarizmi (punim imenom
Abu' Abdallah Muhammad ibn Musa al-Magusi al-Khwarizmi al-Choresmi).
Živio je otprilike 780.g. - 850.g. i bio je učenik u Kući mudrosti, a
kasnije je delovao pred zaštitom kalifa al-Ma'muna. Pisao je o algebri,
geometriji i astronomiji. Al-Khwarizmi
donosi odmak od grčke matematike, koja se većim delom odnosila na geometriju,
prema algebri. Algebra je omogućavala tretiranje racionalnih i iracionalnih
brojeva, geometrijskih veličina i dr. kao algebarskih objekata, što je
dovelo do potpuno novog razvoja matematike. Glavno delo mu je udžbenik
algebre Hisab al-jabr w'al-muqabala. Iz njegovog naziva izvedena je reč
algebra (al jabr). Al-Khwarizmi svojom knjigom želi olakšati rešavanje
svakodnevnih problema (npr. pitanja nasljeđivanja u muslimanskim zakonima),
no prvi deo se može smatrati i ozbiljnije algebarskim: bavi se linearnim
i kvadratnim jednacinama.
Prvi
veliki arapski matematičar je Al-Khwarizmi (punim imenom
Abu' Abdallah Muhammad ibn Musa al-Magusi al-Khwarizmi al-Choresmi).
Živio je otprilike 780.g. - 850.g. i bio je učenik u Kući mudrosti, a
kasnije je delovao pred zaštitom kalifa al-Ma'muna. Pisao je o algebri,
geometriji i astronomiji. Al-Khwarizmi
donosi odmak od grčke matematike, koja se većim delom odnosila na geometriju,
prema algebri. Algebra je omogućavala tretiranje racionalnih i iracionalnih
brojeva, geometrijskih veličina i dr. kao algebarskih objekata, što je
dovelo do potpuno novog razvoja matematike. Glavno delo mu je udžbenik
algebre Hisab al-jabr w'al-muqabala. Iz njegovog naziva izvedena je reč
algebra (al jabr). Al-Khwarizmi svojom knjigom želi olakšati rešavanje
svakodnevnih problema (npr. pitanja nasljeđivanja u muslimanskim zakonima),
no prvi deo se može smatrati i ozbiljnije algebarskim: bavi se linearnim
i kvadratnim jednacinama.
 Al-Karaji
(punim imenom Abu Bekr Muhammad ibn al-Husayn Al-Karaji,
953.g. - 1029.g.),bagdatski matematičar i inžinjer, smatra se prvom osobom
koja je potpuno oslobodila algebru od geometrijskih operacija i zamenila
ih aritmetičkim, što je osnova moderne algebre. Tako npr. svođenje na
potpun kvadrat provodi čisto algebarski.
Al-Karaji
(punim imenom Abu Bekr Muhammad ibn al-Husayn Al-Karaji,
953.g. - 1029.g.),bagdatski matematičar i inžinjer, smatra se prvom osobom
koja je potpuno oslobodila algebru od geometrijskih operacija i zamenila
ih aritmetičkim, što je osnova moderne algebre. Tako npr. svođenje na
potpun kvadrat provodi čisto algebarski.
 Al-Haytham
(punim imenom Abu Ali al-Hasan ibn al-Haytham, 965.g. - 1040.g.)
je verovatno prvi koji je pokušao klasificirati parne savršene brojeve,
kao one oblika 2k-1(2k - 1) gde je 2k - 1 prost broj.
Takođe je prva poznata osoba koja je izrekla Wilsonovu teorema (Ako je
p prost broj, onda p dijeli 1 + (p - 1)!) Nije jasno je li to znao dokazati.
A teorema se zove po Johnu Wilsonu jer mu je njegovo poznavanje (ne i
dokaz) pripisano 1770.g. Prvi poznati dokaz dao je Lagrange 1771.g. Al-Haytham
se bavio i optikom, kvadraturom kruga i sistemima kongruencija.
Al-Haytham
(punim imenom Abu Ali al-Hasan ibn al-Haytham, 965.g. - 1040.g.)
je verovatno prvi koji je pokušao klasificirati parne savršene brojeve,
kao one oblika 2k-1(2k - 1) gde je 2k - 1 prost broj.
Takođe je prva poznata osoba koja je izrekla Wilsonovu teorema (Ako je
p prost broj, onda p dijeli 1 + (p - 1)!) Nije jasno je li to znao dokazati.
A teorema se zove po Johnu Wilsonu jer mu je njegovo poznavanje (ne i
dokaz) pripisano 1770.g. Prvi poznati dokaz dao je Lagrange 1771.g. Al-Haytham
se bavio i optikom, kvadraturom kruga i sistemima kongruencija.
ARAPSKI BROJEVI

Poprilično različiti brojevni sistemi su simultano korišceni na arapskom
poluotoku dugi niz godina.
Postojalo je najmanje 3 različita brojevna sistema:
- računanje na prste: brojevi se pišu rečima; ovaj način računa
su koristili trgovci i računovođe;
- seksagesimalni sistem: brojevi označeni arapskim slovima, koristio
se najčešće za astronomiju;
-indijski dekadni sistem: poznate su preuzete iz Indije,
ali bez standardnog skupa simbola, tako da se u raznim krajevima koristilo
donekle različite oblike poznatih; ispočetka su ih koristili na prašnjavim
pločama koje su omogućavale isto što i danas ploča i kreda;
Poslednji sistem je omogućio napredak numeričkih metoda, npr. računanje
korena (Abu'l-Wafa, Omar Khayyam), otkriće binomnog teoremaa za prirodne
eksponente (al-Karaji), aproksimaciju transcendentnih realnih brojeva
i računanje n-tih korena (al-Kashi).
MATEMATIKA SREDNJOVEKOVNE EVROPE
Smatra se da je srednji vek razdoblje mraka i razdoblje u kojem se nije
događalo ništa važno u naucnom pogledu.
Mladi su europski narodi do kraja 12. veka prihvatili relativno siromašno
starorimsko matematičko nasljeđe: među ostalim tzv. quadrivium koji se
je sastojao od aritmetike, muzike, geometrije i astronomije. Ta su se
otkrica pred imenom ˝matematike˝ često i (zlo)upotrebljavala u astrologiji,
pa nije čudno da neki spisi toga vremena, govoreći o ˝matematičarima i
drugim mračnjacima˝, ne nalaze za njih mnogo lepih reči.
Sve do 11. veka poznavanje Euklidovih ˝Elemenata˝ u Europi je bilo vrlo
oskudno.
Na Siciliji su se neki matematički tekstovi prevodili na latinski i neposredno
s grčkog izvora. U poslednjoj trećini srednjega veka javlja se već nekoliko
»domaćih« europskih matematičara, koji to ime zaslužuju ne samo kao ˝reproizvodivni˝
već i kao ˝kreativni umetnici˝. Među najistaknutije spadaju Fibonacci
i Jordanus Nemorarius.
Pred kraj srednjeg veka matematikom se ozbiljnije bave i neki vrlo istaknuti
nematematičari, posebno slikari, Leonardo da Vinci i Albrecht Dürer, koji
se zauzimaju, pored ostalog, za geometrijske konstrukcije koje se mogu
provesti samo upotrebom šestara s fiksnim otvorom.
Za matematiku je srednji vek u Europi bio tek prelazni period unutar kojeg
su se arapskim posredstvom pomalo učila zaboravljena otkrica starih Grka.
No ta su otkrica poslužila kao odskočna daska za ulaz u matematiku novog
veka Evrope.
U poslednjih pedesetak godina istraživanja su pokazala da je to razdoblje
mnogo bogatije nego što se smatralo, te da je srednji vek vrlo važna spona
između starog i novog veka.
MATEMATIČARI SREDNJOVEKOVNE EVROPE
 Anicius
Manlius Severinus Boethius rođen je oko 480. godine u blizini
Rima. Boetije je bio vrlo dobro školovan. Tečno je govorio grčki i bio
je vrlo dobro upoznat s radom grčkih filozofa, pa povjesničari smatraju
da je studirao u Atini ili Alexandriji, iako za to nema dokaza. Obrazovanje
je Boetiju bilo vrlo važno. Svoj je talenat koristio za pisanje i prevođenje.
Njegovo razumevanje matematike je bilo na vrlo niskom nivou, a i tekstovi
koje je pisao o aritmetici bili su vrlo loši.Naspram tome njegovi matematički
tekstovi bili su najbolji koji su bili dostupni u to vreme i bili su korisceni
mnogo vekova Upravo su Boetijevi tekstovi bili glavni izvor materijala
za quadrivium.
Anicius
Manlius Severinus Boethius rođen je oko 480. godine u blizini
Rima. Boetije je bio vrlo dobro školovan. Tečno je govorio grčki i bio
je vrlo dobro upoznat s radom grčkih filozofa, pa povjesničari smatraju
da je studirao u Atini ili Alexandriji, iako za to nema dokaza. Obrazovanje
je Boetiju bilo vrlo važno. Svoj je talenat koristio za pisanje i prevođenje.
Njegovo razumevanje matematike je bilo na vrlo niskom nivou, a i tekstovi
koje je pisao o aritmetici bili su vrlo loši.Naspram tome njegovi matematički
tekstovi bili su najbolji koji su bili dostupni u to vreme i bili su korisceni
mnogo vekova Upravo su Boetijevi tekstovi bili glavni izvor materijala
za quadrivium.
Postavio je ambiciozan projekt da prevede i napiše komentare na ceo rad
Platona i Aristotela.
Cilj mu je bio pokazati ideje u kojima su se ova dva Grčka filozofa slagala
jedan s drugim. Boetije nije uspeo dovršiti svoj projekt.
Ali je uspeo prevesti na latinski Aristotelove
Categories i De interpretatione. Do 12. veka njegovog dela i prevodi su
bili glavna dela o logici u Europi koja su poznata po imenu Logica vetis,
odnosno stara logika.
Boetije se je bavio i politikom, što ga je dovelo i do optužbe za izdaju,
kao i optužbe za svetogrđe i bavljenje magijom. U zatvoru je napisao svoje
najpoznatije delo De consolatione philosophiae. De consolatione philosophiae
je postala vrlo popularna knjiga u srednjem veku i renesansi.
 Gerbert
je rođen oko 940. godine u Aurillacu, regiji Auvergne, centralna Francuska.
Gerbert
je rođen oko 940. godine u Aurillacu, regiji Auvergne, centralna Francuska.
Gerbert je učio arapske brojeve, tako da je mogao računati u glavi, što
je bilo vrlo teško s rimskim brojevima. Takođe je proučavao abakus, čak
je i konstruiseo jedan divovski. Označio je pred lađe u Reimskoj katedrali
kao abakus i napravio je mnogo velikih diskova umesto zrna abakusa. Skupio
je oko šezdeset i četiri člana katedralske škole da mu pomognu. Dao im
je štapove kojima su gurali diskove, a on je seo na crkveni kor od kuda
je mogao videti ceo pred. On je davao instrukcije, a asistenti su micali
diskove kao da igraju shuffleboard. Na ovaj način je mogao računati s
brojevima manjim i većim od brojeva s kojima se do tada računalo. Nakon
toga je napisao knjigu o abakusu koja je postala standard u novim katedralskim
školama koje su budile i revolucionirale studije matematike na zapadu.
Gerbertovo veliko otkriće je i pronalazenje duzina kateta pravougaonog
trougla kojem je poznata duzina hipotenuze i povrsina.(Iz a2+b2=c2 i ab=2P
tj. a2b2=4P2 proizlazi da su a2, b2 resenja kvadratne jednacine x2-c2x
+4P2=0) .
Gerbert je 999. godine postao papa Sylvester II. Umro je u Rimu 1003.
godine.
Gereard (Gherardo, Gerhard) rođen je 1114. godine u
Cremoni, Italija.
Gerard je preveo oko osamdeset dela s arapskog na latinski jezik. Neka
od tih dela bila su arapska, a neka su bila grčka dela prevedena na arapski.
Ta dela nisu bila sva matematička, bilo je tu medicine i nauke uopsteno.
No najvažnija su bila o astronomiji, geometriji i drugim granama matematike.
. Gerard je preveo Alhvarizijevu algebru te arapski prevod s grčkog Euklidovih
«Elemenata» i Ptolomejeva «Almagesta».
Teško je verovati da je Gerard imao vremena za bavljenjem nečim drugim
osim prevođenjem, zbog veličine posla kojega se je primio, ali ipak je
održavao javna predavanja i imao je reputaciju čoveka od velikoga otkrica.
Jedna od odluka koju je Gerard doneo bila je kod prevođenja arapske reči
za sinus na latinsku riječ sinus. Interesantno je za zaključiti da je
Gerard doneo drugačiju odluku u prevođenju, ova funkcija bila bi poznata
danas pod drugačijim imenom.
Gerard je umro 1187 u Toledu.
MATEMATIKA NOVOG VEKA
Kao što je nekad starogrčka matematika svojim ostvarenjima veoma zasenila
sve što je u toj nauke dotle učinjeno u prijašnjim velikim kulturama Azije
i Afrike, tako je novovekovna matematika Evrope neuporedivo nadmašila
sve što je u matematici dotle bilo ostvareno.
MATEMATIKA DO 20. VEKA
U razdoblju od sredine 17. do sredine 19. veka – dakle unutar nekih dvesta
godina - matematika je obogaćena mnogo više negoli tokom čitava svog dotadašnjeg
razvoja za vreme više od dve hiljade godina. U 17. su veku za matematiku
nastupila, sazreli su uslovi za njen veliki procvat.
U korenima su tog sazrevanja svakako mnoga otkrića koja su tek pripremila
put za kasniji gotovo eksplozivni rast: bez tih otkrića do njega ne bi
bilo došlo.
NOVA OTKRIĆA
Algebra je zakoračila daljim koracima napred kada su tri italijanska renesansna matematičara nasla resenje kubne jednacine. Matematičari renesanse znaju da se svaka kubna jednacina moze svesti na oblik bez kvadratnog člana putem linearne supstitucije. Stoga je dovoljno znati resiti jednacine oblika x3+px+q=0. Napomenimo jos i da u renesansi, iako su ponegde poznati, negativni brojevi jos nisu opsteprihvaćeni te su stoga u renesansnom shvatanju jednacine x3+px=q i x3=px+q različiti tipovi kubne jednacine.
POZNATI MATEMATIČARI
Za razvoj algebre tokom renesanse posebno je zaslužan poznati francuski
matematičar koji to nije bio, FrançoisViète (1540.-1603.) koji je po struci
bio pravnik.
Kao matematičar iz hobija, dvaput se našao u prilici pomoći svojoj državi
otkricem matematike.
Prvi put bilo je to kad je španski kralj Filip II., poznati borac protiv
reformacije, zagovornik inkvizicije i pokretač armade protiv Engleske,
1590. godine postavio zahtev za francuskim prestolom na osnovi rodbinskih
veza. Tadašnji francuski kralj Henrik IV., protestant, odbija zahteve
te dolazi do rata. U tom ratu slane su razne šifrirane poruke te iz tog
doba potiče jedna od najpoznatijih matematičkih anegdota iz kriptografije.
Francuzi su presreli jednu špansku poruku te ju je kralj dao Vièteu da
je dešifrira. To Viète i uspeva, Španjolcima postaje jasno da Francuzi
znaju za njihove namjere, a Filip II. tužio je Francusku papi da se koristi
crnom magijom.
Viète je počeo razvijati i ˝tehničko računanje˝ s algebarskom notacijom
– ne samo da se proizvoljna i nepoznata veličina označavala slovom, već
se s takvim slovima počelo i manipulisati. U svojem delu ˝In artem analyticam
isagoge˝ (1591) Viete upotrebljava samoglasnike za nepopoznatice, a suglasnike
za poznate, date veličine.
 Descartes,
veliki filozof (1596.-1650.) upotrebio je (već od pre poznatu) metodu
koordinatnog proučavanja ovisnosti jedne veličine (funkcije) o drugoj
(varijabli) da bi povezao geometriju s algebrom: geometrijska su se pitanja
sada mogla formulisati, izučavati i rešavati algebarskim sredstvima, a
algebarske veze mogle su se ilustrovati geometrijski.
Descartes,
veliki filozof (1596.-1650.) upotrebio je (već od pre poznatu) metodu
koordinatnog proučavanja ovisnosti jedne veličine (funkcije) o drugoj
(varijabli) da bi povezao geometriju s algebrom: geometrijska su se pitanja
sada mogla formulisati, izučavati i rešavati algebarskim sredstvima, a
algebarske veze mogle su se ilustrovati geometrijski.
Pascal je bio ˝ čudo od deteta˝ od rane mladosti. S dvanaest
godina sam je ponovno otkrio mnogo toga iz elementarne geometrije. Sa
četrnaest godina već je prisustvovao sastancima francuskih matematičara
koji su kasnije stvorili Francusku akademiju. No bio je slabogzdravlja
i s 27 godina napustio je (iako ne zauvek) matematička istraživanja i
posvetio se gotovo potpuno religioznim razmišljanjima. Pred kraj svog
kratkog života napisao je glasovite ˝Pensées˝ (˝Misli˝), možda jedno od
najvrednijih dela francuske književnosti.
Gottfried Wihelm Leibniz (1646-1716) bio je ne samo jedan
od najvećih matematičara, već i jedan od najvećih filozofa svoga doba
(teorija monada!). Većinu kapitalnih matematičkih dela, poznatih u njegovoj
mladosti, proučio je Leibniz dok mu nije bilo još ni dvadeset godina.
MATEMATIKA 20. VEKA
U ovom razdoblju razvila su se mnoga predručja matematike kao što su
teorija verovatnosti, matematička logika, teorija skupova te infinitezimalni
račun. Za poslednjih stotinak godina stvoreno je u matematici više od
svega onoga što je stvoreno u čitavoj istoriji te nauke do početka toga
razdoblja.
Matematika 20. veka beleži veliki broj poznatih matematičara koji su uvelike
doprineli onom što danas nazivamo modernom matematikom.
NOVA OTKRIĆA
Teorija skupova predstavlja važan temelj matematike, a trenutno se najviše vezuje uz matematičku logiku. Njena istorija bitno se razlikuje od istoriji ostalih predručja matematike. Mnoge grane matematike dugo su se razvijale dokle god njihove ideje ne bi evoluirale do ultimatnog «flasha» ili inspiracije, najčešće doprinosom većeg broja matematičara koji bi, većinom istovremeno, došli do «otkrića» istaknute vrednosti. S druge strane, teorija skupova nastala je zahvaljujući jednom čoveku – Georgu Cantoru, da bi tek kasnije, od 1890. do 1930. postala središnjim predmetom matematičkih rasprava.
Pojam „infinitezimal“ predstavlja broj koji je beskonačno malen, a ipak veći od nule. Začeci ovog pojma sežu još iz antike, Aristotel (utemeljitelj sistematske logike) prognao je iz geometrije beskonačno maleno i veliko, no do punog procvata infinitezimalnog rasuđivanja došlo je s generacijama nakon Pascala: Newtonom, Leibnizom, braćom Bernoulli i Leonhardom Eulerom.
POZNATI MATEMATIČARI
 Albert
Einstein (Ulm,1879. - 1955.), fizičar-teoretičar i najistaknutiji
stvaratelj novog doba u fizici.
Albert
Einstein (Ulm,1879. - 1955.), fizičar-teoretičar i najistaknutiji
stvaratelj novog doba u fizici.
Sve do svoje treće godine Albert nije progovorio, ali je pokazivao neverovatnu
radoznalost i briljantnu moć shvaćanja kompliciranih matematičkih koncepata.
U doba od 12 godina sam je sebe naučio geometriju. Otkrio je niz osnovnih
zakona prirode (brzinu svetlosti kao maksimalnu brzinu, dilataciju vremena
i novu interpretaciju dilatacije dužina, te ekvivalentnost mase i energije,
korpuskularnu prirodu svetlosti i princip ekvivalencije te osnovu opste
teorije relativnosti).
Einstenovo najpoznatije delo je teorija relativnosti koja je ne samo od
osnovne važnosti kao temeljni okvir za daljnji razvoj teorijske fizike,
već duboko zahvata i u filozofske koncepcije, o prostoru i vremenu, a
povrh toga u probleme kosmologije i kosmogonije.
 Georg
Ferdinand Ludwig Philipp Cantor (1845.Vek Petersburg, Russia
–1918. Halle, Germany) bio je nemački matematičar. Najpoznatiji je kao
osnivač teorije skupova. Uspostavio je važnost bijekcije među skupovima,
definisao beskonačne i dobro uređene skupove. Definisao je kardinalne
i ordinalne brojeve i njihovu aritmetiku. Bio je prvi koji je proučavao
hipotezu kontinuuma koja se bavi tezom da ne postoji skup čija je snaga
veća od skupa prirodnih brojeva, a manja od skupa realnih brojeva.
Georg
Ferdinand Ludwig Philipp Cantor (1845.Vek Petersburg, Russia
–1918. Halle, Germany) bio je nemački matematičar. Najpoznatiji je kao
osnivač teorije skupova. Uspostavio je važnost bijekcije među skupovima,
definisao beskonačne i dobro uređene skupove. Definisao je kardinalne
i ordinalne brojeve i njihovu aritmetiku. Bio je prvi koji je proučavao
hipotezu kontinuuma koja se bavi tezom da ne postoji skup čija je snaga
veća od skupa prirodnih brojeva, a manja od skupa realnih brojeva.
Hilbert je za njega rekao:˝Niko nas ne sme izbaciti iz raja koji je Cantor
stvorio˝.
David Hilbert (1862.-1943.) bio je nemački matematičar,
prepoznat je kao jedan od najuticajnijih matematičara 20-tog veka. Otkrivao
je i razvijao veliki spektar funadamentalnih matematičkih ideja. Bavio
se funkcionalnom analizom, sa naglaskom na Hilbertovom prostoru.
Takođe je poznat kao jedan od osnivača dokazne teorije te matematičke
logike..
John Forbes Nash rođen je 1928. u Zapadnoj Virdziniji.
Na sveučilištu Princeton, u vreme kad su tamo radili naucnici poput Alberta
Einsteina i Johna von Neumanna, bio je smatran čudom od deteta. Već pre
navršene 30. godine bio je poznat na Princetonu i kasnije matematičkom
odseku na MIT-u po sposobnosti razumevanja i rešavanja teških matematičkih
problema koji su za njegove kolege bili gotovo nerešivi. Njegov je najveći
doprinos na predručju teorije igre koja je revolucionalizirala
ekonomiju, a izneo ju je u svojoj disertaciji od 27 stranica "Nekooperativne
igre" koju je napisao u doba od 21 godine. Postao je izvanredni profesor
u svojim 20-tim godinama i smatrali su ga genijem.
1958., u doba od 30 godina, neposredno pre nego što je trebao postati
redovni profesor na MIT-u obolio je od paranoidne shizofrenije s bizarnim
iluzijama. Napustio je MIT i sledećih je 30 godina u mnogo navrata hospitalno
lečen, često i protiv svoje volje. 1994. godina, kad je imao 66 godina,
njegovo se psihičko stanje stabilizovalo, ušao je u remisiju, a istovremeno
i nenadano dodeljena mu je Nobelova nagrada za ekonomiju.
Prema njegovoj biografiji "Beautiful Mind" Sylvije Nasar snimljen
je istoimeni film koji je dobitnik 4 Oskara za 2001. godinu.
LITERATURA
1. Stefan Barker,
Filozofija matematike
Beograd, 1973.2. Mirko Dejić
Tajni svet matematike
Nolit, Beograd, 1990.3. Vladimir Devidé
Matematika kroz kulture i epohe
Školska knjiga, Zagreb, 1979.4. Lanselot Hogben
Stvaranje matematike
Vuk Karadžić, Beograd, 1972.5. Mala enciklopedija PROSVETA
Prosveta, Beograd, 1972.6. http://www.matf.bg.ac.yu/~zlucic/zlucic.html
preuzmi
seminarski rad u wordu » » »


