OSTALI SEMINARSKI RADOVI
IZ MATEMATIKE: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Istorija logaritama
Matematički problemi, bez obzira koliko izgledali apstraktni, imaju svoju
osnovu u svakodnevnim ljudskim potrebama. Ustvari, može se, veoma grubo,
reći da je skoro svaki problem koji se javi i matematički problem. Svaka
grana nauke koristi bar jedno matematičko otkriće, odnosno rešenje nekog
matematičkog problema.
Da ova tvrdnja nije preterana pokazuju mnogi primeri, koji su ostali zapisani
u istoriji (udvostručavanje kocke, kvadratura kruga, merenje rastojanja,
konstrukcije itd.)
Ovde ćemo se posebno osvrnuti na značaj otkića logaritama, kao jedan od
najubedljivijih dokaza o primeni matematike. Njihova popularnost, krenuvši
od astronomije pa sve do finansija je prosto zapanjujuća.
Pojava logaritama dovela je do jedne male revolucije (ili evolucije) ne
samo u matematici, već i u nauci uopšte.
Prvi radovi
Veoma je teško reći kada se razmišljanje ove vrste prvi put pojavilo,
verovatno zato što se nagoveštavalo u radovima mnogih matematičara. Prilaz
temi je uzet, kao i danas, iz relacije ![]() , za koju je znao čak i Arhimed.
, za koju je znao čak i Arhimed.
Ustvari, ideja je potekla iz posmatranja dvojnih nizova. Neka su data
dva niza
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
... |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
... |
gde je prvi aritmetički, a drugi geometrijski. Može se uočiti da za geometrijski
niz važi sledeće: 2![]() ,
2
,
2![]() ,
2
,
2![]() ,
2
,
2![]() ,
2
,
2![]() ,
2
,
2![]() ,
2
,
2![]() ,
2
,
2![]() ,
... . Daljim razmatranjem, mogu se izvesti sledeća pravila:
,
... . Daljim razmatranjem, mogu se izvesti sledeća pravila:
2![]() ·2
·2![]() =2
=2![]() 2
2![]() :
2
:
2![]() =2
=2![]() ( 2
( 2![]() )
)![]() =2
=2![]() ( 2
( 2![]() )
)![]() =2
=2![]() ,
,
što su ustvari fundamentalni zakoni logaritama.
Većina pisaca pripisuje Stifelu, da je prvi obznanio i veoma precizno
objasnio ova četiri pravila. Međutim, radovi na ovu temu postojali su
i pre njega. Verovatno najbolji izveštaj koji se tiče ovih zakona, pojavio
se u petnaestom veku, tačnije 1484 godine, od strane Cuqueta u delu Le
Triparty en la Science des nombres. Na osnovu njega je Estienne de
la Roche objavio svoj rad Larismethique
. Cuquet je dosta detaljno pojasnio relacije
![]()
![]()
u vezi sa dvojnim nizovima, za koje su ova pravila i bila izvedena, obraćajući
posebnu pažnju na zakon poznat kao ' tajna ' proporcionalnih brojeva.
Sledeće delo u nizu, koje je ostavilo upečatljiv trag, nastalo je od strane
Rudolffa 1526 godine, po imenu Kunstliche rechnung, gde su data
sva četiri pravila u vezi sa dvojnim nizovima. Ovaj rad uticao je na Stifela
da 1544 godine objavi rad Arithmetica Integra. Važno je napomenuti,
a to je i najveća Stifelova zasluga, da su u njemu data i pravila koja
se odnose i na negativne vrednosti eksponenta.
Međutim, mnogo ljudi je bilo inspirisano radovima Rudolffa i Stifela,
kao što su Jacob, Clavius i Apianus. Prvi aritmetičar koji je imao viziju
o važnosti ovih relacija bio je Gemma Frisius, i dao je nekoliko zakona
o dvojnim nizovima oblika
3 |
9 |
27 |
81 |
243 |
729 |
... |
0 |
1 |
2 |
3 |
4 |
5 |
... |
U kasnijim radovima nemačkih i francuskih matematičara vidi se da oni poznaju problematiku i razvijali su razne teorije, ali ništa značajnije se nije dogodilo do objave Bürgijevog rada.
Veliko otkriće
Dva švajcarska matematičara sedamnaestog veka zaslužili su veliku pažnju
– jedan je bio genije, a drugi plagijator. Genije je bio Joost Bürgi,
najveštiji i najpoznatiji časovničar svoga vremena. Rođen je 28 februara
1552 godine u Lichtensteigu.
 U
periodu od 1579 do 1603 godine radio je u službi Landgrafa Wilhelma IV,
a kasnije (nakon 1622) u službi Kaisera Rudolpha II. Svoju veštinu je
upotrebio i na pravljenje izvanrednih naučnih instrumenata. Pisao je o
proporcionalnim kompasima i o astronomiji, a tek kasnije se javila njegova
zainteresovanost za matematiku. Koliko je ozbiljna bila njegova namera
i želja da produbi znanja iz matematike, pokazuje i činjenica da je Johaness
Kepler, tada carski matematičar, bio zadužen da ga uputi u pojmove algebre.
Verovatno je Kepler
i podstakao Bürgija da objavi svoje originalno i izvanredno delo
o logaritmima. Godine 1620, publikovane su, u Pragu, njegove tablice Progress
Tabulen . Tablice su bile liste antilogaritama sa osnovom 1.0001.
U
periodu od 1579 do 1603 godine radio je u službi Landgrafa Wilhelma IV,
a kasnije (nakon 1622) u službi Kaisera Rudolpha II. Svoju veštinu je
upotrebio i na pravljenje izvanrednih naučnih instrumenata. Pisao je o
proporcionalnim kompasima i o astronomiji, a tek kasnije se javila njegova
zainteresovanost za matematiku. Koliko je ozbiljna bila njegova namera
i želja da produbi znanja iz matematike, pokazuje i činjenica da je Johaness
Kepler, tada carski matematičar, bio zadužen da ga uputi u pojmove algebre.
Verovatno je Kepler
i podstakao Bürgija da objavi svoje originalno i izvanredno delo
o logaritmima. Godine 1620, publikovane su, u Pragu, njegove tablice Progress
Tabulen . Tablice su bile liste antilogaritama sa osnovom 1.0001.
Logaritmi su štampani u crvenoj boji (prvi gornji red i prva leva kolona),
a antilogaritmi u crnoj boji, zbog čega je Bürgi svoje logaritme zvao
Die Rothe Zahl. Na slici se može videti jedan segment ovih tablica.
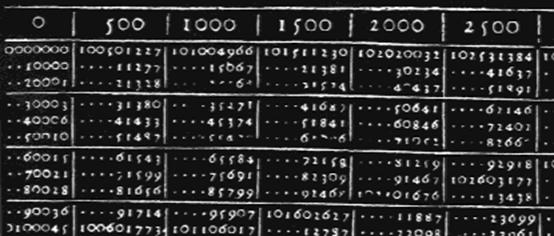
deo rukopisa iz dela Progress Tabulen.
U to vreme, iako značajan, njegov rad je prošao prilično nezapaženo. Preminuo
je 31 januara 1632 u Kasselu, koji danas pripada Nemačkoj. Njegovi originalni
rukopisi sačuvani su u Pulkowoj observatoriji. Jedine sačuvane tablice
antilogaritama pripadaju izvesnom Jamesu Dodsonu.
Pojam logaritma
Reč logaritam je kovanica dve grčke reči logos (logos – ratio) i aritmos
(arithmos – broj). Tvorac ovog termina, kao i samog pojma logaritma je
John Napier. U njegovim ranijim rukopisima mogao se susresti izraz ' veštački
broj ' (artifical number).
 Kao
i njegov savremenik Bürgi, Napier nije bio profesionalni matematičar već
škotski lord, baron od Merchistona. Rođen je 1550 u Merchistonskom dvorcu
u okolini Edinburgha, u vreme velikih borbi između katolika i protestanata
u Skotskoj. O njegovoj ranoj mladosti zna se veoma malo. Iz pisma njegovog
oca Archibalda, orkneyskom biskupu, može se naslutiti da je Napier neko
vreme boravio u inostranstvu.
Kao
i njegov savremenik Bürgi, Napier nije bio profesionalni matematičar već
škotski lord, baron od Merchistona. Rođen je 1550 u Merchistonskom dvorcu
u okolini Edinburgha, u vreme velikih borbi između katolika i protestanata
u Skotskoj. O njegovoj ranoj mladosti zna se veoma malo. Iz pisma njegovog
oca Archibalda, orkneyskom biskupu, može se naslutiti da je Napier neko
vreme boravio u inostranstvu.
Sa trinaest godina pohađao je St. Andrew Univerzitet, gde se, kako on
sam kaže, zainteresovao za teologiju. Verovatno je to bio razlog zbog
čega je za svoje najveće delo smatrao The Plaine Discovery of the
Whole Revelation of Saint John, gde je dokazivao da je rimski papa
Antihrist, odnosno nevernik. Ipak, Napierova genijalnost se ipaik najsnažnije
ispoljila kroz njegove matematičke radove.U Edinburghu, godine 1614, u
delu Mirifici Logarithmorum Canonis Descriptio obznanjuje javnosti
svoje otkriće.
Mnogo pre, procenjuje se negde oko 1588, započeo je njegov rad na problemu
logaritama. Ustvari, Napierova najveća preokupacija bila je trigonometrija.
Ideja, koja ga je vodila ka rešavanju problema, je bila da pojednostavi
množenje sinusa
. Tek kasnije, upotrebu logaritama proširiće na brojeve.
Za razliku od današnjeg shvatanja pojma logaritma, koji kao i kod Bürgija
bio algebarski, Napier je problematici pristupio sa geometrijske tačke
gledišta. Da bi smo što bolje razumeli njegovu definiciju logaritama,
moramo znati neke osnovne činjenice. U to vreme sina je posmatran kao
duž, a ne kao razlomak. Prečnik r se nazivao sinus totus,
i ako je on bio jedinstvene dužine, za dužinu sinusa se prosto uzimalo
sina. Ali ako on nije bio jedinstvene dužine, onda je za dužinu sinusa
uzimano r ·sina.
 Logaritmi
koje je Napier izveo nisu imali bazu, odnosno bar mu to nije bila namera,
ali se sa današnje tačke gledišta može, dosta grubo, reći da je ta osnova
postojala i iznosila je otprilike 1/e.
Logaritmi
koje je Napier izveo nisu imali bazu, odnosno bar mu to nije bila namera,
ali se sa današnje tačke gledišta može, dosta grubo, reći da je ta osnova
postojala i iznosila je otprilike 1/e.
Pogledajmo sada definiciju koja se pojavila u delu Descriptio
:
' Neka je data duž AB i poluprava A'X. Tačke C i C' počinju da se kreću
od tačka A i A', respektivno, u isto vreme, udesno. Tačka C se kreće sa
ravnomernim ubrzanjem, dok se tačka C' kreće sa ubrzanjem koje odgovara
rastojanju CB. Rastojanje A'C' zove se logaritmom rastojanja BC. '
 Da
bi sačuvao manja rastojanja u geometrijskoj progresiji koja nastaje, za
dužinu AB koristio je vrednost 10
Da
bi sačuvao manja rastojanja u geometrijskoj progresiji koja nastaje, za
dužinu AB koristio je vrednost 10![]() .
Ovo je sasvim razumljivo, jer da bi članovi geometrijskog niza ostali
na relativno malim rastojanjima, potrebno je da prvi član bude veoma blizak
jedinici. Napier je za ovu vrednost uzimao 1 - 10
.
Ovo je sasvim razumljivo, jer da bi članovi geometrijskog niza ostali
na relativno malim rastojanjima, potrebno je da prvi član bude veoma blizak
jedinici. Napier je za ovu vrednost uzimao 1 - 10![]() .
Da bi izbegao računanje sa decimalama on je svaki član niza množio sa
10
.
Da bi izbegao računanje sa decimalama on je svaki član niza množio sa
10![]() .
Tako, ako bi važilo N=10
.
Tako, ako bi važilo N=10![]() (1-1/10
(1-1/10![]() )
)![]() ,
onda je broj L Napierov logaritam broja N. Odavde se može primetiti da
je (1-1/10
,
onda je broj L Napierov logaritam broja N. Odavde se može primetiti da
je (1-1/10![]() )
)![]() vrlo blisko lim n ® ¥ ( 1 - 1/n )
vrlo blisko lim n ® ¥ ( 1 - 1/n )![]() ,
što je jednako 1/e. Iz ovoga je veoma razumljivo što se prirodni logaritmi
zovu hiperbolički ili Napierovi, iako on za njih nije znao. U reizdanju
prevoda Edwarda Wrightsa, 1618 godine, u dodatku koji je verovatno napisao
Oughtred, pojavljuje se izraz log
,
što je jednako 1/e. Iz ovoga je veoma razumljivo što se prirodni logaritmi
zovu hiperbolički ili Napierovi, iako on za njih nije znao. U reizdanju
prevoda Edwarda Wrightsa, 1618 godine, u dodatku koji je verovatno napisao
Oughtred, pojavljuje se izraz log![]() 10=2.302584,
u kome se prepoznaje baza e. Dve godine kasnije John Speidell u svom izdanju
New Logarithmes , takođe koristi ovu bazu i navodi sledeće:
10=2.302584,
u kome se prepoznaje baza e. Dve godine kasnije John Speidell u svom izdanju
New Logarithmes , takođe koristi ovu bazu i navodi sledeće:
logn = 10![]() ( nap log1 – nap logn ),
( nap log1 – nap logn ),
logn = 10![]() ( 10 + log10
( 10 + log10![]() x
).
x
).
Osim tablice logaritama, Napier je izneo i neka pravila logaritama, ali
preko proporcija:
- ako je a : b = c : d, onda logb – loga = logd – logc.
- ako je a : b = b : c, onda logc=2logb - loga.
- ako je a : b = b : c, onda 2logb=loga + logc.
- ako je a : b = c : d, onda logd = logb + logc – loga.
- ako je a : b = c : d, onda logb + logc = loga + logd.
- ako je a : b = b : c = c : d, onda 3logb = 2loga + logd i
3logc = loga + 2logd.
Veza između sinusa i njegovog logaritma u Napierovom sistemu je data
formulom:
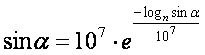 .
.
Starost je sprečila Napiera da dalje razvije svoje logaritme. Preminuo
je 4 aprila 1617 u Edinburghu, iste godine kada je izašlo i njegovo poslednje
delo Rhabdologia, u kome je dao opis svojih štapića za računanje.
Proširena tablica logaritama, izdata je posthumno, 1619 godine u delu
Mirifici ipsius canonis constructio, kao dodatak drugom izdanju
rada Descriptio.
Razvoj logaritama
Čovek, koji je od samog početka pratio Napiera do njegovog uspeha bio
je Henry Briggs (1561 – 1630). Bio je poznat kao prvi profesor geometrije
na Gresham koledžu od 1596 do 1619, a kasnije profesor geometrije i astronomije
na Oxfordu. Koliko je bilo njegovo oduševljenje kada je pročitao Descriptio
vidi se iz sledećeg odlomka iz pisma, koje je upućeno James Ussheru, 10
marta 1615:
' Napier, lord of Markinston, hath set my head and hands at work with
his new and admirable logarithms. I hope to see him this summer, if it
please God; for I never saw a book which pleased me better, and made me
more wonder. '
 Naredne
godine 1616, on je posetio Edinburgh u nameri da se sretne sa Napierom.
To je bila jedna od prvih poseta u kojima je Briggs, za osnovu, predložio
broj 10, o čemu je Napier već razmišljao. Po povratku u Oxford, 1617 godine,
objavljuje svoje prvo delo o logaritmima pod nazivom Logarithmorum
Chilias Prima. Sledeće njegovo važnije delo o logaritmima, u kojem
se za osnovu pojavljuje broj 10
, je Arithmetica Logarithmica sive Logarithmorum Chiliades Triginta
izdato je
1624 godine, od strane Vlacqa. U njemu je Adriaan Vlacq dodao i logaritme
za brojeve od 20 000 do 90 000, pošto je Briggs dao vrednosti logaritama
za brojeve od 1 do 20 000 i 90 000 do 100 000. Pri izradi ovih tablica
Briggsu je pomogao njegov kolega i prijatelj Henry Gellibrand. Deo ovih
tablica pojavljuje se i u delu Trigonometria Britannica (1633).
Naredne
godine 1616, on je posetio Edinburgh u nameri da se sretne sa Napierom.
To je bila jedna od prvih poseta u kojima je Briggs, za osnovu, predložio
broj 10, o čemu je Napier već razmišljao. Po povratku u Oxford, 1617 godine,
objavljuje svoje prvo delo o logaritmima pod nazivom Logarithmorum
Chilias Prima. Sledeće njegovo važnije delo o logaritmima, u kojem
se za osnovu pojavljuje broj 10
, je Arithmetica Logarithmica sive Logarithmorum Chiliades Triginta
izdato je
1624 godine, od strane Vlacqa. U njemu je Adriaan Vlacq dodao i logaritme
za brojeve od 20 000 do 90 000, pošto je Briggs dao vrednosti logaritama
za brojeve od 1 do 20 000 i 90 000 do 100 000. Pri izradi ovih tablica
Briggsu je pomogao njegov kolega i prijatelj Henry Gellibrand. Deo ovih
tablica pojavljuje se i u delu Trigonometria Britannica (1633).
Veza između Napierovih i Briggsovih logaritama se može prikazati na sledeći
način:
Napier, logy = r·( logr – logy ) , gde je r =10![]() ;
;
Briggs, logy = 10(10 – logy ) .
Briggs je do kraja svog života objavio deset radova, a još šest je ostalo neobljavljeno. Publikovani radovi ticali su se problema navigacije (Tables for the Improvement of Navigation), Euklidovih Elemenata i trigonometrije.
Dalje širenje logaritama
Benjamin Ursinus (1507 – 1634), profesor matematike na Univerzitetu u
Frankfortu, bio je jedan od prvih matmatičara koji je kroz svoja dela
Trigonometria logarithmica, Magnus canon triangularum logarithmicas
predstavio pojam logaritma u Nemačkoj.
U Danskoj, zasluge za popularizaciju logaritama zaslužan je Niculaus Mercator
(1610 – 1687). Interesovao se za kosmografiju, a njegova najvažnija dela
u vezi logaritamskog računa su Logarithmotechnia (1668) i Methodus
construendi logarithoms nova accurata et facilis. U prvoj knjizi,
sproveo je u delo jednu zamisao njegovog brata, da logaritam predstavi
preko redova a to je poznata jednakost
log( ![]() +a
) = a –
+a
) = a – ![]() a
+
a
+ ![]() a
–
a
– ![]() a
+ ...
a
+ ...
gde je ![]() a
a
![]()
![]() .
.
Za širnje logaritama u Kinu, zaslužni su jezuiti. Prve rasprave o ovoj
temi objavio je Sié Fong-tsu 1650 godine, učenik poljskog jezuite Johna
Nicolasa Smogolenskog. Tek 1713 godine, u Pekingu su odštampane prve logaritamske
tablice, i interesantno je pomenuti da su to bile Vlacqove tablice iz
1628 godine.
Takođe je bitno reći, da su svi ovi događaji uticali, krenuvši od Keplera,
na buduće radove astronoma naročito u izradi astronomskih tablica, koje
su u mnogome olakšale merenje rastojanja u vasioni.
Literatura
1. History of Mathematics I , by David Euegene Smith ( 1958 )
2. History of Mathematics II, by David Euegene Smith ( 1958 )
3. http://www-groups.dcs.st-andrews.ac.uk/čhistory/Mathematicians
4. http://www.micheloud.com/FXM/LOG/
5. http://www-math.sci.kun.nl/math/werkgroepen/gmfw/bronnen
preuzmi
seminarski rad u wordu » » »


