OSTALI SEMINARSKI RADOVI
IZ MATEMATIKE: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
KRUG I NJEGOVA SVOJSTVA
“Prava i krug” ( kružna linija, kružnica ) jesu od najstarijih vremena glavne linije u geometriji. Njihov značaj proizilazi iz njihove jednostavnosti i iz mnogobrojnosti njihovih lako uočljivih osobina i primena, ali takođe i otud što se krug i prava mogu najjednostavnije konstruisati: napr. prava lenjirom, a krug šestarom. Ove dve sprave uticale su bitno na razviće geometrije u Starom veku i na utvrđivanje njenog sadržaja.''[3, str.194] Geometrijske konstrukcije u ravni koje možemo izvršiti pomoću lenjira i šestara smatramo elementarnim.Krug je jedna od najinteresantnijih i najznačajnijih geometrijskih figura. Konstruisanje ostalih figura ne može se ni zamisliti bez krugova (čitajte šestara), pa su stoga krug (odnosno kružna površ), centar i poluprečnik u Euklidovim ''Elementima'' uvodeni na početku, definicijama:
''15. Krug je ravana figura omeđena takvom jednom linijom (koja se zove periferija), da su sve prave povučene od jedne tačke, koja se nalazi u samoj figuri, prema toj liniji (prema periferiji kruga) međusobno jednake.
''16. Ova tačka zove se središte kruga.
''17. Prečnik kruga je svaka prava što prolazi kroz središte kruga a ograničena je sa svake strane periferijom kruga; on polovi krug.''[5, str.5]
''Euklid se već u prvim stavovima ''Elemenata'' služi krugom da bi konstruisao podudarne duži. Sam krug je lik zasnovan na podudarnosti. I definicija kruga bi se mogla izreći tako da se neposredno pominju podudarne duži: ''Ukupnost tačaka jedne ravni, koje su jedni krajevi svih među sobom jednakih duži, kojima je drugi kraj izvesna tačka te ravni, nazivamo krugom.'' No definicija je jednostavnija ako se primeni izraz ''jednako udaljeno'' koji uvodimo definicijom:''[3, str.194/5]
2. Pojam kruga
Definicija 2.1: Krug k predstavlja skup tačaka u ravni podjednako udaljenih od neke fiksne tačke O.
Tačku O zovemo središte ili centar kruga, a svaku duž koja spaja središte sa ma kojom tačkom kruga poluprečnikom ili radijusom kruga k. Za krug kome je središte tačka O kažemo i da je opisan oko tačke O.

Tvrđenje 2.1: Kod svakog kruga k centar O i poluprečnik r su jednoznačno određeni.

Definicija 2.2: Za unutrašnje tačke poluprečnika
jednog kruga i za središte tog kruga kažemo da su u krugu, a za one tačke
u ravni kruga koje ne pripadaju krugu niti su u njemu kažemo da su van
kruga.
Definicija 2.3: Skup svih tačaka na krugu
i tačaka u njemu nazivaćemo ravna kružna površ, kraće kružna
površ.
Teorema 2.1: Svaka prava koja je u ravni kruga
k i prolazi kroz njegovo središte, ima sa krugom k dve zajedničke tačke.
Dokaz: Neka je p bilo koja prava u ravni
kruga k, koja prolazi kroz njegovo središte O, i neka
je OA bilo koji njegov poluprečnik. Sa svake strane tačke O postoji po
jedna tačka na p, dakle svega dve tačke, recimo
P i P¢, takve da su duži OP i OP¢ jednake poluprečniku OA tog kruga. To
su prema definiciji 2.1 tačke zajedničke s krugom k.
Dakle postoje na p svega dve takve tačke, sa
svake strane tačke O po jedna.
Teorema 2.2: Na svakoj pravoj koja je
u ravni jednog kruga i koja prolazi kroz njegovo središte postoji duž
čiji su krajevi tačke toga kruga, a središte tog kruga je središte te
duži.
Definicija 2.4: Duž koja spaja dve tačke
kruga i pri tome sadrži središte kruga naziva se prečnik
ili dijametar.
Teorema 2.3: Svaki krug ima beskonačno mnogo tačaka.

Dokaz: Neka je k bilo koji krug u jednoj ravni a i O njegovo središte. Neka je a prava u istoj ravni a, koja ne prolazi kroz O. Prema [3, teorema 6.5] ima na a beskonačno mnogo tačaka, na pr. beskonačan niz tačaka A1, A2, A3, ... . Prema tome kroz tačku O postoji beskonačno mnogo pravih OA1, OA2, OA3, ... , raznih među sobom i koje su u ravni a. Prema teoremi 2.1 svaka takva prava ima s krugom po dve zajedničke tačke i neka su to: prava OA1 dve tačke B1 i B1¢, OA2 tačke B2 i B2¢, OA3 tačke B3 i B3¢ itd. Odavde sledi da krug ima beskonačno mnogo tačaka.
3. Tetiva i sečica kruga
Definicija 3.1: Duž koja spaja ma koje dve tačke kruga zove se tetiva. Tetiva koja sadrži središte kruga je dijametar ili prečnik.
Teorema 3.1: Prečnici su najveće tetive.
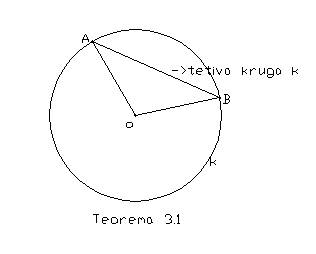
Dokaz: Prema definicijama 2.1 i 2.3 prečnici su tetive.
Neka je AB tetiva kruga koja nije prečnik, tj. koja ne sadrži središte
O kruga . Tada postoji trougao ABO, koji je jednakokrak, jer je prema
definiciji 2.1 OA=OB. Prema [3, teorem 26.17] je OA+OB>AB. No zbir
OA+OB jednak je prečniku, dakle tetiva AB je manja od prečnika, i prema
tome prečnici su najveće tetive.
Teorema 3.2: Svaka sečica ima s krugom dve i
samo dve zajedničke tačke.
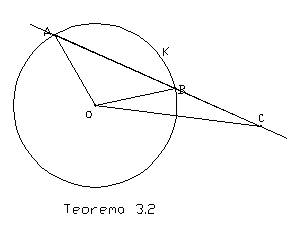
Dokaz: Pretpostavimo, naprotiv, da sečica AB, koja
ima sa krugom dve zajedničke tačke A i B, ima s njim još jednu zajedničku
tačku C. Prema [3, teorema 6.8] jedna od tačaka A, B, C je između ostale
dve. Neka je napr. A-B-C. Kako je prema definiciji OA=OB=OC, trougli OAB
i OBC su jednakokraki, dakle prema [3, teorema 22.8] je ![]() OAB=
OAB=![]() OBA
i
OBA
i ![]() OBC=
OBC=![]() OCB.
Ti uglovi su oštri, jer trougao ne može imati dva prava ili dva tupa ugla.
Ali
OCB.
Ti uglovi su oštri, jer trougao ne može imati dva prava ili dva tupa ugla.
Ali ![]() OBA
i
OBA
i ![]() OBC
su dva naporedna ugla, dakle postojala bi dva oštra naporedna ugla, a
to je nemoguće.
OBC
su dva naporedna ugla, dakle postojala bi dva oštra naporedna ugla, a
to je nemoguće.
Teorema 3.3: Unutrašnje tačke tetive su u krugu.
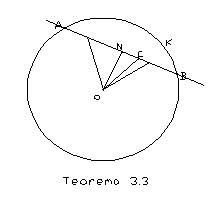
Dokaz: Ako je tetiva prečnik kruga, teorema sledi
neposredno iz definicija 2.2 i 2.3. Neka je zato AB tetiva manja od prečnika
i O središte kruga i neka je ON normalna iz O na pravu AB, N njeno podnožje.
Neka je zatim C ma koja druga unutarnja tačka tetive AB . Prema[3, teorema
25.18] je ON<OA, dakle prema prema definiciji 2.2 N je u krugu. Kako
se duž AB sastoji iz duži AN i BN, C je tačka jedne ili druge od ove dve
duži, tj. imamo A-C-N ili B-C-N, dakle prema [3, definicija 25.1] je CN<AN,
odnosno CN<BN, dakle prema [3, teorema 25.18] je CO<AO u oba slučaja,
jer je AO=BO. Prema tome C je u krugu.
Teorema 3.4: Prava koja je u ravni jednog kruga,
a prolazi kroz krajnju tačku jednog njegovog poluprečnika i gradi s njim
kos ugao, jeste sečica toga kruga.

Dokaz: Neka je p prava
u ravni kruga k opisanog oko tačke O, A tačka kruga kroz
koju prolazi p i neka su uglovi između p
i poluprečnika OA kosi ( jedan oštar, drugi tup). Tada je normala ON spuštena
iz O na pravu p različita od OA. Neka je N njeno
podnožje, a B tačka na p za koju je A-N-B i
AN=BN. Trouglovi OAN i ONB su podudarni, jer je AN=BN, ON=ON, ![]() ONA=
ONA=![]() ONB
( pravi uglovi) dakle je i OA=OB. tj. prema definiciji 2.1 je i B tačka
kruga k. Dakle, prema definiciji 2.3 prava p
je sečica kruga k.
ONB
( pravi uglovi) dakle je i OA=OB. tj. prema definiciji 2.1 je i B tačka
kruga k. Dakle, prema definiciji 2.3 prava p
je sečica kruga k.
4. Tangenta kruga
Definicija 4.1: Prava koja je u ravni jednog kruga, a ima sa njom samo jednu zajedničku tačku naziva se tangenta toga kruga, a ta tačka zove se dodirna tačka ili tačka dodira.
Teorema 4.1: Kroz svaku tačku kruga prolazi jedna i samo jedna tangenta. Ona je normalna na poluprečnik koji prolazi kroz tu tačku a njene ostale tačke su van kruga.
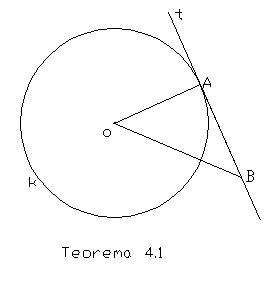
Dokaz: Neka je A tačka kruga opisanog oko tačke O . Prema [3,
teorema 23.7] postoji u ravni kruga jedna i samo jedna prava t
normalna na pravoj CA i koja prolazi kroz tačku A. Neka je B druga tačka
na t. Prema [3, teoremi 25.18] je OA<OB,
dakle prema definiciji 2.2 tačka B je izvan k. Prema
tome A je jedina tačka prave t, koja pripada
krugu, tj. t je tangenta. Neka je p
bilo koja druga prava koja prolazi kroz tačku A. Ona nije normalna na
OA u tački A, jer t je jedina takva prava, dakle
p gradi sa OA kose uglove, te je prema teoremi
3.4 sečica, i prema tome nije tangenta. Dakle kroz svaku tačku kruga k
prolazi jedna i samo jedna tangenta. Po pretpostavci t
je normalna na poluprečniku OA, koja prolazi kroz dodirnu tačku A.
Teorema 4.2: Prava koja je u ravni kruga, a prolazi
kroz krajnju tačku jednog njegovog prečnika, i gradi s njim prav ugao,
je tangenta tog kruga.
Dokaz: Neka je, kao u prethodnom dokazu, t
ta prava, A tačka kruga kroz koju prolazi t
, O središta kruga. Ako je opet B ma koja druga tačka prave t,
prema [3, teorema 25.18] je OB>OA, dakle tačka B je van kruga, tj.
A je jedina tačka prave t, zajednička sa krugom.
Dakle, prava t je prema definiciji 2.4 tangenta
kruga k.
Definicija 4.2: Ugao koji zahvataju dva kruga
koja se seku u nekoj tački G, zvaćemo ugao koji zahvataju
tangente tih krugova u tački G.
Ugao koji zahvataju prava i krug koji se seku u tački G, zvaćemo ugao
koji zahvataju ta prava i tangenta kruga u tački G.
Za dva kruga ili za pravu i krug reći ćemo da su upravni,
normalni ili ortogonalni ako zahvataju
prav ugao.
Teorema 4.3: Ako su t
i t¢ dve tangente
istog kruga, koje prolaze kroz jednu istu tačku B izvan kruga, tada su:
1) duži od tačke B do dodirnih tačaka jednake i
2) oštri uglovi koje obrazuju obe tangente s polupravom koja spaja tačku
B sa središtem tog kruga, jednaki.
Dokaz: Neka su dodirne tačke A i A¢ . Prava OB nije tangenta, jer
prema teoremi 2.1 ima s krugom dve zajedničke tačke, dakle tačke A i A¢
nisu na pravoj OB i prema tome postoje trouglovi ABO i A¢BO. Ti trouglovi
su podudarni, jer je OA=OA¢, OB=OB i ∡OAB=∡OA¢B ( pravi uglovi), a uglovi
naspram stranica OA i OA¢ su oba oštra. Dakle imamo AB=A¢B i ∡ABO=∡A¢BO.
Teorema 4.4: Kroz svaku tačku tangente jednog
kruga, različitu od dodirne tačke, može se povući još jedna i samo jedna
tangenta istoga kruga.
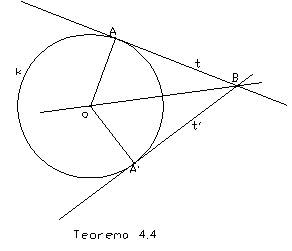
Dokaz: Neka je t tangenta, kruga k
opisanog oko tačke O i neka je A dodirna tačka , a B bilo koja druga tačka
prave t. Prema [3, teorema 21.2] postoji u ravni
kruga, s one strane prave OB s koje nije A, poluprava BC sa početkom B,
tako da je ![]() ∡OBA=
∡OBA=![]() OBC.
Neka je na polupravoj BC tačka A¢ takva da je AB=A¢B, prema [3,teorema
20.6] postoji samo jedna takva tačka. Kako su A i A¢ sa raznih strana
prave OB, to su dve različite tačke. Trouglovi OAB i OA¢B su dakle razni,
a podudarni su, jer je AB=A¢B, OB=OB,
OBC.
Neka je na polupravoj BC tačka A¢ takva da je AB=A¢B, prema [3,teorema
20.6] postoji samo jedna takva tačka. Kako su A i A¢ sa raznih strana
prave OB, to su dve različite tačke. Trouglovi OAB i OA¢B su dakle razni,
a podudarni su, jer je AB=A¢B, OB=OB, ![]() OBA=
OBA=![]() OBA¢,
pa je OA=OA¢ i
OBA¢,
pa je OA=OA¢ i ![]() OAB=
OAB=![]() OA¢B.
Dakle, prema definiciji 2.1 tačka A¢ krugu k. Kako je
t tangenta,
OA¢B.
Dakle, prema definiciji 2.1 tačka A¢ krugu k. Kako je
t tangenta, ![]() OAB
je prema teoremi 4.1 prav ugao, dakle i
OAB
je prema teoremi 4.1 prav ugao, dakle i ![]() OA¢B
je prav ugao, te je prema teoremi 4.2 i prava AB tangenta na k,
tj. kroz tačku B postoji još jedna tangenta. Prave AB i A¢B su jedine
tangente na k kroz tačku B. Zaista, pretpostavimo da
je A¢¢B treća tangenta s dodirnom tačkom A¢¢. Prema teoremi 4.3 je AB=A¢¢B;
uz to je OA=OA¢¢. Dakle, ako je tačka A¢¢ s one strane prave OB s koje
je tačka A, prema [3, aksioma III 4] je A¢¢≡A. Ako je pak s one strane
prave OB s koje je A¢, tada je A¢¢≡A¢, tj. nepostoji treća različita tangenta.
OA¢B
je prav ugao, te je prema teoremi 4.2 i prava AB tangenta na k,
tj. kroz tačku B postoji još jedna tangenta. Prave AB i A¢B su jedine
tangente na k kroz tačku B. Zaista, pretpostavimo da
je A¢¢B treća tangenta s dodirnom tačkom A¢¢. Prema teoremi 4.3 je AB=A¢¢B;
uz to je OA=OA¢¢. Dakle, ako je tačka A¢¢ s one strane prave OB s koje
je tačka A, prema [3, aksioma III 4] je A¢¢≡A. Ako je pak s one strane
prave OB s koje je A¢, tada je A¢¢≡A¢, tj. nepostoji treća različita tangenta.
5. Centralni ugao kruga
Definicija 5.1: Ugao u ravni jednog kruga, kome je teme središte kruga naziva se centralni ugao tog kruga.
Ako su A i B one tačke na kracima oštrog središnjeg ugla, koje pripadaju samom krugu, reći ćemo da tetiva AB i taj centralni ugao odgovaraju jedan drugome.
Segment AB toga kruga i njegov komplement zvaćemo lukovima toga kruga.Ako luk AB pripada uglu AOB, reći ćemo da je tada luk AB zahvaćen tim centralnim uglom.
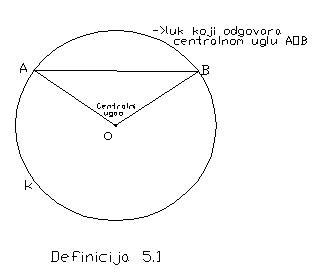
Teorema 5.1: Jednakim tetivama jednog
kruga odgovaraju jednaki centralni uglovi, jednakim centralnim uglovima
odgovaraju jednake tetive i obratno.
Dokaz: Neka su AB i CD dve tetive kruga opisanog oko tačke O i
neka je AB=CD. Kako je i OA=OC, OB=OD, trouglovi OAB i OCD su podudarni,
dakle je i ![]() AOB=
AOB=![]() COD.
Obrnuto: ako je
COD.
Obrnuto: ako je ![]() AOB=
AOB=![]() COD,
iz OA=OC i OB=OD, sledi da su trouglovi OAB i OCD podudarni, dakle da
je AB=CD.
COD,
iz OA=OC i OB=OD, sledi da su trouglovi OAB i OCD podudarni, dakle da
je AB=CD.
6. Periferijski ugao kruga
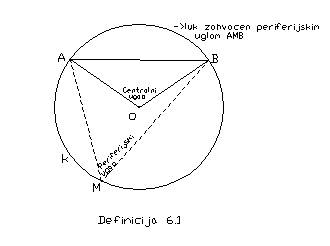
Definicija 6.1: Ako je M proizvoljna tačka kruga k različita od A i B, konveksan ugao AMB zvaćemo periferijskim uglom tog kruga, a ugao AOB zvaćemo odgovarajućim centralnim uglom nad tom tetivom.
Ako luk AB pripada tom uglu, reći ćemo da je tada luk zahvaćen tim periferijskim uglom.
Stav 6.1: Neka je AB prečnik kruga
sa centrom u tački O i poluprečnikom r, i neka je P proizvoljna tačka
toga kruga različita od A i B. Tada je ugao APB prav, i tačka O predstavlja
centar opisanog kruga oko pravouglog trougla APB, i nalazi se na središtu
hipotenuze tog trougla.
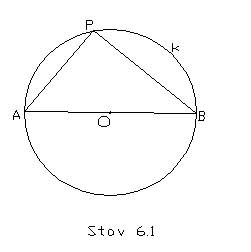
Dokaz: S obzirom da su trouglovi OPA i OPB jednakokraki, uglovi na osnovicama su im podudarni prema [1,teorema 11.12] i jednaki su polovinama njima
nesusednih spoljašnjih uglova BOP i AOP. Zbir uglova BOP i AOP je p, pa će zbir uglova APO i BPO biti p/2. Dakle ugao APB je prav.
Teorema 6.1: Periferijski ugao kruga jednak je polovini njegovog centralnog ugla koji zahvata isti luk toga kruga.
Dokaz: Neka su A, B i C tri razne tačke kruga sa centrom u tači O i poluprečnikom r, a D tačka dijametralno suprotna tački C. Trouglovi OAC i OBC su jednakokraki, pa će zato uglovi na osnovicama biti podudarni [1,teorema11.12]. Budući da je spoljašnji ugao trougla jednak zbiru dvaju unutrašnjih nesusednih uglova, biće ÐAOD=2ÐACD, i ÐBOD=2ÐBCD. Zavisno od toga da li su tačke A i B sa iste ili sa raznih strana prave CD, ugao AOB biće jednak razlici ili zbiru uglova AOD i BOD, a ugao ACB razlici ili zbiru uglova ACD i BCD. Stoga je ÐAOB=2ACB. Ista relacija će važiti i ako su tačke C, O, B kolinearne.
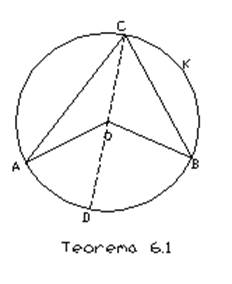
Važi i obrnuto, ako su ACB i ADB dva podudarna ugla kojima su temena C i D sa iste strane prave AB , tada postoji krug koji sadrži tačke A, B, C i D. Zaista, ako su krugovi koji sadrže trojke tačaka A, B, C i A, B, D mađusobno različiti, tada će središta O i O’ tih dvaju krugova da budu dve razne tačke koje pripadaju medijatrisi duži AB. Ako je S središte duži AB, uglovi AOS i AO’S neće biti podudarni, pa ni njihovi periferijski uglovi ACB i ADB neće biti podudarni. Kontradikcija!
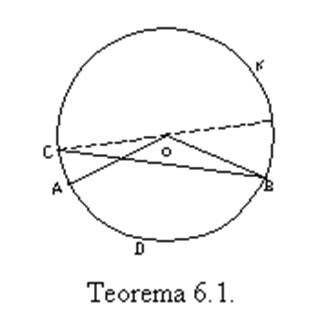
Teorema 6.2: Svi periferijski uglovi jednog kruga koji zahvataju isti luk međusobno su podudarni.
7.
Potencija tačke u odnosu na krug
Teorema 7.1: Neka je P proizvoljna tačka neke ravni koja ne pripada zadatom krugu k te ravni, a p i q prave koje sadrže P takve da p seče krug k u tačkama A i B, a q u tačkama C i D. Tada je PA·PB=PC·PD. Ako je P izvan kruga k, a T dodirna tačka kruga k i tangente koja sadrži P, tada je PA·PB=PT2.
Dokaz: Ako je tačka P izvan kruga k,
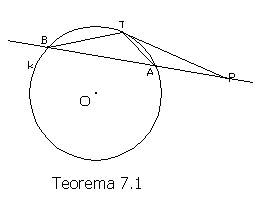
trouglovi PAT i PTB će biti slični, pa je
![]()
a odavde sledi da je PA·PB=PT2.
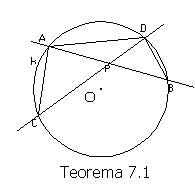
trouglovi PBC i PDA su slični jer su uglovi jednog podudarni uglovima drugog pa je
![]()
Dakle, PA·PB=PC·PD.
Proizvod PA·PB koji zavisi samo od tačke P i kruga k, nazivamo potencijom tačke P u odnosu na krug k. Primetimo da se u prethodnom razmatranju ništa neće promeniti ako pretpostavimo da su PA i PB mere orjentisanih duži.
Tada je proizvod PA·PB pozitivan ili negativan u zavisnosti od toga da li su te dve duži istosmerne ili nisu, pa je, zato, tačka P izvan kruga k ako i samo ako je proizvod PA·PB pozitivan.
Teorema 7.2: Skup p svih tačaka zadate ravni kojima su potencije u odnosu na dva kruga k(O, r) i k'(O', r'), O≠O', međusobno jednake, je prava upravna na pravoj OO'.
Dokaz: Ako tačka P pripada skupu p, na osnovu Pitagorine teoreme biće
OP2-r2=O'P2-r' 2, pa je OP2- O'P2= r2- r' 2. Ako je Q podnožje upravne iz tačke P na pravoj OO’, opet na osnovu Pitagorine teoreme biće
OQ²-O'Q²=OP²-O'P²=r²-r' ²
.
Dakle tačka P pripada pravoj koja je u tački Q upravna na OO'.
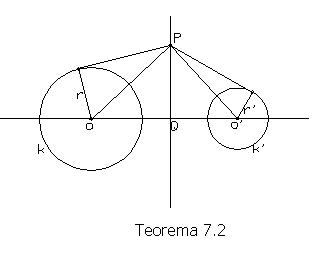
Obrnuto, ako tačka P pripada pravoj koja je u tački Q upravna na pravoj
OO', tada je OP2= OQ2+PQ2 i O'P2 = O'Q2+PQ2, pa je OP2- O'P2 = OQ2- O'Q2
= r2- r' 2. Zato je
OP2- r2= O'P2- r' 2
pa je potencija tačke P u odnosu na krug k jednaka potenciji iste tačke
u odnosu na krug k'.Dakle, p je prava u tački Q upravna na pravoj OO'.
8. Radikalna osa kruga
Definicija 8.1:Prava koja se sastoji od tačaka
koje imaju jednake potencije u odnosu na zadate krugove naziva se radikalna
osadvaju krugova.
Razlikujemo tri slučaja:
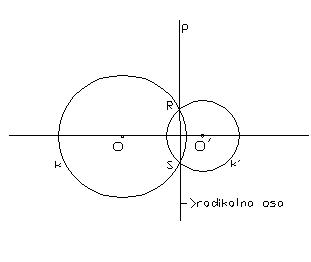
1.Krugovi se seku- njihova radikalna osa sadrži
presečne tačke tih dvaju krugova
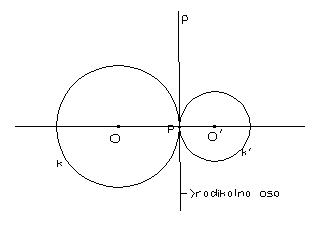
2. Krugovi se dodoruju- njihova radikalna osa je zajednička tangenta tih dvaju krugova u njihovoj dodirnoj tački.
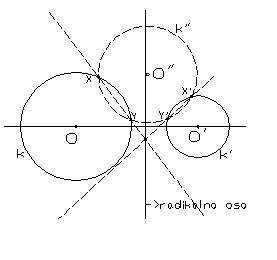
3. Krugovi su disjunktni-dovoljno je odrediti jednu tačku radikalne ose. Da bi se ona odredila zadati krugovi se preseku trećim krugom i presečne tačke jednog od tih krugova sa trećim krugom obeležimo sa X i Y, a drugog sa X' i Y'. Presek pravih XY i X'Y' je tačka koja pripada radikalnoj osi.
9.
Pramenovi krugova
Definicija 9.1: Skup svih krugova jedne ravni od kojih svaka dva za radikalnu osu imaju istu pravu zvaćemo sistemom koaksijalnih krugova ili pramenom krugova. Skup središta svih krugova jednog pramena pripada jednoj pravoj i ta prava je osa pramena.
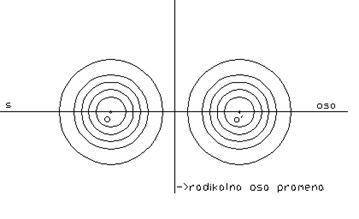
Teorema 9.1: Svaki pramen je jednoznačno određen sa dva svoja kruga.
Razlikujemo tri vrste pramena krugova s obzirom na međusobni odnos odgovarajućih krugova u okviru pramena:
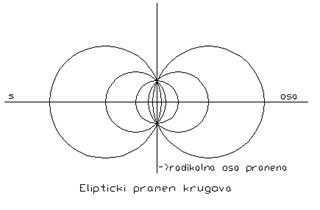
1.Ako se svaka dva kruga pramena seku u dvema različitim tačkama, takav pramen nazivamo eliptičkim.
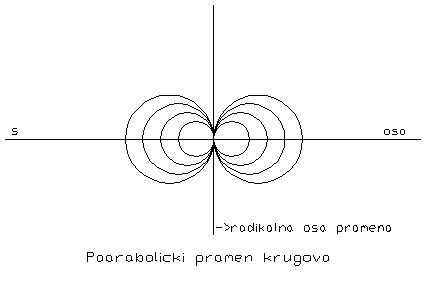
2. Ako se svaka dva kruga pramena dodiruju u istoj tački, takav pramen krugova nazivamo paraboličkim.
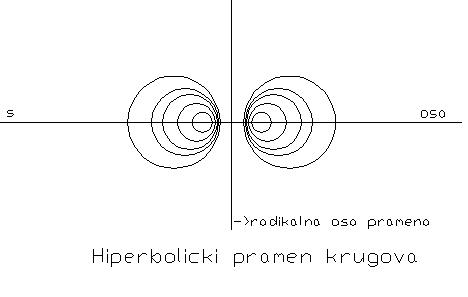
3. Ako su svaka dva kruga pramena disjunktna, takav pramen krugova nazivamo hiperboličkim.
4. Ako su ose dvaju pramena krugova međusobno upravne,
onda ćemo ta dva pramena krugova zvati međusobno upravnim
pramenovima.
10. Inverzija u odnosu na krug
Neka je dat krug k(O,r) koji pripada ravni α. Reći ćemo da se tačka ![]() (različita od O) inverzijom ψ u odnosu na krug k(O,r) preslikava u tačku P' ako su O, P i P' tri kolinearne tačke takve da je
(različita od O) inverzijom ψ u odnosu na krug k(O,r) preslikava u tačku P' ako su O, P i P' tri kolinearne tačke takve da je
OP·OP'=r².

Za tačku P' reći ćemo da je inverzna tački P u odnosu na krug k(O,r), a taj krug ćemo zvati i krugom inverzije ψ. Tačku O ćemo zvati središte inverzije. Iz definicije neposredno sledi da je inverzija bijektivno preslikavanje definisano na ravni α bez tačke O. Ako je tačka P' inverzna tački P, tada je i tačka P inverzna tački P', pa je, zato, inverzija involucij. Tačka unutar kruga k (različita od O) se inverzijom preslikava u tačku van kruga, a tačka van kruga u tačku unutar toga kruga. Tačka će pripadati krugu inverzije ako i samo ako je u toj inverziji invarijantna.
Ako je tačka P unutar kruga k(O,r) i ako je T tačka u kojoj prava koja sadrži P i upravna je na pravoj OP, seče k, onda tangenta kruga k u tački T seče pravu OP u nekoj tački P'. Tada su trouglovi OPT i OTP' slični, pa je
![]() .
.
Dakle, OP·OP'=OT²=r², pa je tačka P' inverzna tački P.
Ako je P' izvan kruga k(O,r), krug čiji je prečnik OP' seče krug k u nekoj tečki T. Ugao OTP' je prav pa je podnožje upravne prave iz T na pravoj OP' tačka P koja pripada duži OP'. Opet će trouglovi OPT i OTP' biti slični, pa će biti OP·OP'=OT²=r². Dakle, tačka P biće inverzna tački P'.
Terema 10.1: Proizvod dveju inverzija u odnosu na koncentrične krugove k(O,r) i k'(O,r') je homotetija sa koeficijentom(r'/r)².
Dokaz: Ako se tačka P preslikava prvom inverzijom u P', a P' drugom inverzijom u P'', tada je OP·OP'=r² i OP'·OP''=r'², pa proizvod zadatih inverzija preslikava tačku P u tačku P'' takvu da je
![]() .
.
Teorema 10.2: Ako sadrži središte inverzije, prava se inverzijom preslikava na sebe, a ako ne sadrži središte inverzije, preslikava se na krug kome nedostaje središte inverzije.
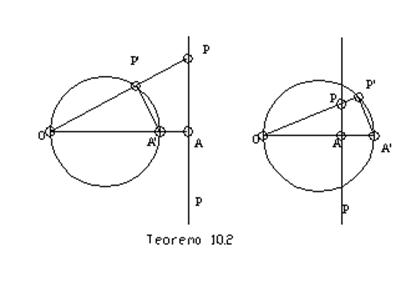
Dokaz:Iz definicije inverzije neposredno sledi da se prava koja
sadrži središte inverzije preslikava u istu pravu. Pretpostavimo da prava
p ne sadrži središte inverzije-tačku O. Neka je A podnožje upravne prave
iz tačke O na pravu p, neka je A' slika tačke A u zadatoj inverziji, a
P' slika bilo koje tačke P zadate prave p. Tada je
OP·OP'=r²=OA·OA',
pa su trouglovi OAP i OP'A' slični budući da imaju jedan ugao zajednički.
Kako je ugao OAP prav, i ugao OP'A' biće prav, pa tačka P' pripada krugu
čiji je prečnik OA'.
Obrnuto, ako je P' tačka kruga čiji je prečnik OA', ugao P'OA' biće oštar,
pa prava koja sadrži tačku A i upravna ja na pravoj OA seče polupravu
OP' u nekoj tački P. Tada su trouglovi OAP i OP'A' slični, pa je OP·OP'=OA·OA'.
Dakle, tačka P je slika tačke P' u zadatoj inverziji.
Teorema 10.3: Ako sadrži središte O inverzije,
krug (kome nedostaje tačka O) se preslikava na pravu, a ako ne sadrži
središte inverzije, krug se preslikava na krug.
Dokaz:Videti u [1] strana 229.
U posebnom slučaju kada krug sa središtem C sadrži dve inverzne tačke,
tada se on, na osnovu 7.1, inverzijom preslikava na sebe. Tada će prava
koja sadrži središte inverzije i presek T kruga inverzije i kruga sa središtem
C biti upravna na pravoj CT, pa će ti krugovi biti upravni. Obrnuto, kada
je krug sa središtem C upravan na krugu inverzije taj krug se inverzijom
preslikava na sebe.
- ZORAN LUČIĆ, Euklidska i hiperbolička geometrija, Total design i matematički fakultet, Beograd, 1997. god.
- G. KALAJDŽIĆ, M. ĐORIĆ, Skripta iz osnova geometrije, Matematički fakultet, Beograd, 2002. god.
- MILOŠ RADOJČIĆ, Elementarna geometrija osnove i elementi euklidske geometrije, Naučna knjiga, Beograd, 1961. god.
- EUKLID, Elementi, Naučna knjiga, Beograd, 1957.god.
preuzmi
seminarski rad u wordu » » »



